Posts filed under Risk (222)

TV3 has tried to stir up the issue of the death penalty in New Zealand.  They have a poll showing majority opposition by the country as a whole, and by supporters of every party except NZ First.  Even the Sensible Sentencing Trust isn’t in favor.

The lead-in to the story is that the murder rate has never ‘recovered’ from the abolition of the death penalty.  They have a graph showing homicides per capita rising and then falling again, but not to the earlier levels.

Using the term ‘recovered’ comes very close to asserting a causal connection; but is there even a reliable correlation? International comparisons are useful here.  I don’t have long time series for homicide, but Kieran Healy has produced a graph of international trends in deaths due to assault. This isn’t the same as homicide, but is close enough to be relevant.

Here’s the New Zealand panel, with the arrow indicating the abolition of the death penalty. The details are slightly different from those for homicide, but the basic trend is the same that TV3 reports.

and here’s the international comparison, with NZ second from the bottom, on the left. As usual, click to embiggen

The NZ pattern is very similar to other countries, including Australia (where abolition didn’t happen until about 10 years later), Finland (where it was abolished in 1949 for crimes committed in peacetime), and Switzerland (1942).

If you look at the countries that still have the death penalty, murder rates are low and falling in Japan, South Korea had the same sort of rise and fall that NZ has had (over a shorter time scale), and of course there’s the USA.

It doesn’t look as though the death penalty is a major driving force in these patterns.

From a number of fields

• The WiFi system at the British Library wouldn’t let a researcher get to an online copy of Hamlet, because of the violent content. “The site is dismal, and our affairs from England come too late”
• From one of the Guardian’s science blogs: [update: link fixed]

So when one particular paper began to strain the servers, attracting hundreds if not thousands of downloads, the entire editorial board began to pay attention. “What,” they asked, “is so special about this paper on the ryanodine receptor of Caenorhabditis elegans?” (For those of you who don’t know, Caenorhabditis elegans is a very common and much-loved model animal—it’s a small, soil-living roundworm with some very useful features. Please don’t ask me what a ryanodine receptor is; I don’t know and I don’t really care.)

• Along similar lines, someone reminded me of the problem the UK town of Scunthorpe has with text filtering.  There is an old joke that there are two other football teams whose names contain swear words (punchline)

Nate Silver’s talk at the Joint Statistical Meetings a couple of weeks ago identified groupthink by insiders as a major threat to accurate journalism.  It’s natural to believe the opinions of other intelligent, well-informed people, but if they are working from  the same limited set of information as you, the fact that they agree with you is not actually good evidence that you’re right.

Tim Harford has a column this week arguing that diversity is important, for basically this reason. Even if, say, women or Maori or Asians or small-town farm boys aren’t actually better at decision-making, the simple fact that they have different starting points can lead to better decision-making by groups. It doesn’t have to, but it can. The New York Times also has a piece on this theme, by political scientist Scott Page.

An important empirical basis for the idea that diversity is, in itself, beneficial is the work of Solomon Asch on conformity.  Asch found that even in very simple decisions, many people would follow an obviously-wrong choice made by enough other people. On the other hand, even a single non-conforming voice, and even one that was more wrong than the consensus, could free people to follow the evidence of their own eyes.

There’s a long tradition in law and ethics of thinking about how much harm to the innocent should be permitted in judicial procedures, and at what cost. The decision involves both uncertainty, since any judicial process will make mistakes, and consideration of what the tradeoffs would be in the absence of uncertainty. An old example of the latter is the story of Abraham bargaining with God over how many righteous people there would have to be in the notorious city of Sodom to save it from destruction, from a starting point of 50 down to a final offer of 10.

With the proposed new child protection laws, though, the arguments have mostly been about the uncertainty.  The bills have not been released yet, but Paula Bennett says they will provide for protection orders keeping people away from children, to be imposed by judges not only on those convicted of child abuse but also ‘on the balance of probabilities’ for some people suspected of being a serious risk.

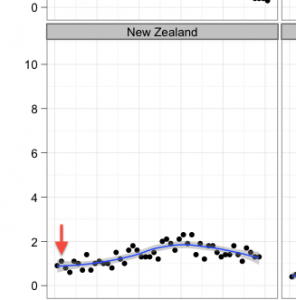
We’ve had two stat-of-the-week nominations for a blog post about this topic (arguably not ‘in the NZ media’, but we’ll leave that for the competition moderator). The question at issue is how many innocent people would end up under child protection orders if 80 orders were imposed each year.

The ‘balance of probabilities’ standard theoretically says that an order can be imposed (?must be imposed) if the probability of being a serious risk is more than 50%.  The probability could be much higher than 50% — for example, if you were asked to decide on the balance of probabilities which of your friends are male, you will usually also be certain beyond reasonable doubt for most of them.  On the other hand, there wouldn’t be any point to the legislation unless it is applied mostly to people for whom the evidence isn’t good enough even to attempt prosecution under current law, so the typical probabilities shouldn’t be that high.

Even if we knew the distribution of probabilities, we still don’t have enough information to know how many innocent people will be subject to orders. The probability threshold here is the personal partly-subjective uncertainty of the judge, so even if we had an exact probability we’d only know how many innocent people the judge thought would be affected, and there’s no guarantee that judges have well-calibrated subjective probabilities on this topic.

In fact, the judicial system usually rules out statistical prior information about how likely different broad groups of people are to be guilty, so the judge may well be using a probability distribution that is deliberately mis-calibrated.  In particular, the judicial system is (for very good but non-statistical reasons) very resistant to using as evidence the fact that someone has been charged, even though people who have been charged are statistically much more likely to be guilty than random members of the population.

At one extreme, if the police were always right when they suspected people, everyone who turned up in court with any significant evidence against them would be guilty.  Even if the evidence was only up to the balance of probabilities standard, it would then turn out that no innocent people would be subject to the orders. That’s the impression that Ms Bennett seems to be trying to give — that it’s just the rules of evidence, not any real doubt about guilt.  At the other extreme, if the police were just hauling in random people off the street, nearly everyone who looked guilty on the balance of probabilities might actually just be a victim of coincidence and circumstance.

So, there really isn’t an a priori mathematical answer to the question of how many innocent people will be affected, and there isn’t going to be a good way to estimate it afterwards either. It will be somewhere between 0% and 100% of the orders that are imposed, and reasonable people with different beliefs about the police and the courts can have different expectations.

Stats Chat reader Elizabeth Paton-Simpson emailed us about what would have been a worthy Stat of the Week nomination. It’s from back in June, so isn’t eligible, but I wanted to share it with you:

Elizabeth wrote the following to the Sunday Star Times:

An item in the Sunday Star Times on 2 June was headlined: “Anaesthetics triple risk of dementia for elderly”. Likewise, the opening paragraph proclaimed: “Having a general anaesthetic may triple the risk of dementia in elderly patients, a study suggests.”

Trained to be sceptical of media claims, I read on and found reference only to a 35 percent increase. Checking the purported source revealed that the Sunday Star Times had altered the summary in The Times from “may increase … by a third” to “may triple”. So please tell Grandma she need not be alarmed – it’s just another example of journalistic innumeracy.

The Sunday Star Times responded:

Yes, you’re correct that the Times later corrected their article however we took their wire service copy which originally said “triple”. I’m sorry for any alarm this may have caused! And, of course, you are right that this should have been picked up in our subbing process.

Unfortunately, the statistic remains uncorrected elsewhere, such as The Australian.

Every year, the Discovery Channel has “Shark Week”, which is apparently their top-rated week of the year.  This year they led off with a programme about the extinct shark C. megalodon, which made the great white shark look like a guppy.

Unfortunately, they did a “Does Megalodon still exist?” programme.  The answer is, definitively, “No”, and to get any other answer you’d have to make up some evidence. That didn’t put them off.  Read Christie Wilcox (scientist) and Wil Wheaton (celebrity nerd) for more.

The excuse for putting this on StatsChat is below

I suppose it’s appropriate that they use a bogus poll to try to prove they fooled most of the people who trust them for science communication.

An excellent long piece about lotteries, from the online magazine Nautilus.  There are many viewpoints presented, including one from the president of the Tennessee lottery corporation

Hargrove has an intuitive understanding of what drives her customers to play the game. She has a preternatural sense of where their psychological buttons are located and how to push them. She responded in a flash to my comment about the logical futility of playing the lottery. “If you made a logical investment choice, you’d play a different game,” she said, leaning forward for emphasis. “It’s not an investment. It’s entertainment. For a very small amount of money you might change your life. For $2 you can spend the day dreaming about what you would do with half a billion dollars—half a billion dollars!”

When  both payoffs and odds that are beyond any conceptual understanding you could do a simple expected-value calculation and label government lotteries as a tax on stupidity, but that framing assumes lottery players are calculating the expected payoff and just getting it wrong. Empirically, it seems to be more complicated than that.

Collapsing lots of variables into a single ‘goodness’ score always involves choices about how to weight different information; there isn’t a well-defined and objective answer to questions like “what’s the best rugby team in the world?” or “what’s the best university in the world?”.  And if you put together a ranking of rugby teams and ended up with Samoa at the top and the All Blacks well down the list, you might want to reconsider your scoring system.

On the other hand, it’s not a good look if you make a big deal of holding failing schools accountable and then reorder your scoring system to move a school from “C” to “A”. Especially when it’s a charter school founded by a major donor to the governing political party.

Emails obtained by The Associated Press show Bennett and his staff scrambled last fall to ensure influential donor Christel DeHaan’s school received an “A,” despite poor test scores in algebra that initially earned it a “C.”

“They need to understand that anything less than an A for Christel House compromises all of our accountability work,” Bennett wrote in a Sept. 12 email to then-chief of staff Heather Neal, who is now Gov. Mike Pence’s chief lobbyist.

We have seen before on StatsChat that, worldwide, there’s no relationship between the position of the moon and the risk of earthquakes.  Suppose, for the sake of argument, that there was some relationship in New Zealand.  Imagine that in Wellington, 100% of big earthquakes happened in the 24-hour period centered on the moon’s closest approach to the earth. The real figure is more like 0%, since Sunday’s earthquake missed the window by a few hours (perigee was 8:28am Monday) and the 1855 Wairarapa quake and the 1848 Marlborough quake missed by days, but we’re running a thought experiment here.  Would this level of prediction be useful?

At one or two big quakes per century, even if they all happened on a predictable day of the lunar month, that’s a risk of between 0.075% and 0.15% per month. At one extreme, you couldn’t evacuate Wellington every month to get around the risk (and even if you did, it would probably cause more injuries each month than happened in Sunday’s quake).  At the other extreme, you could make sure you had a few days supply of water and food, and a plan for communicating with friends and relatives, but that’s a good idea even in the real world where earthquakes are unpredictable.  The only thing I could think of is that you wouldn’t schedule major single-day tourist events (World Cup games, royal visits) or the most delicate pieces of construction work for that day.

[If you want to look up lunar distances, there’s a convenient online calculator. Note that the times are in UTC, so the NZ standard time is 12 hours later than given]

In what may be the least accurate risk estimate ever published in a major newspaper, the Daily Mail said last week

• Hormone replacement could cause meningioma in menopausal women
• Those using HRT for a decade have a 70% chance of developing a tumour
• Most are benign but 15% are malignant and all have damaging side effects

You don’t actually need to look up any statistics to know this is wrong, just ask yourself how many women you know who had brain surgery. Hormone replacement therapy was pretty common (until it was shown not to prevent heart disease), so if 70% of women who used it for a decade ended up with meningioma, you’d know, at a minimum, several women who had brain surgery for cancer.  Do you?

In fact, according to the British NHS, the lifetime risk of meningioma is about 0.07%. Since it’s more common in women, that might be as much as 0.1% lifetime risk for women. The research quoted by the Mail actually found a relative risk of 1.7, so the lifetime risk might be up to 0.17% in women who take a decade of hormone replacement therapy. That is, the story overestimates the risk by 69.8 percentage points, or a factor of more than 400.

While this may be a record so far, there’s still room for improvement, and I certainly wouldn’t bet on the record standing for ever.

(via @hildabast and @BoraZ on Twitter, and Paul Raeburn of the MIT science journalism program)