Posts filed under Random variation (139)

From Stuff

The road toll has moved into triple figures for 2014 following the deadliest April in four years.

Police are alarmed by the rising number of deaths, that are a setback after the progress in 2013 when 254 people died in crashes in the whole year – the lowest annual total since 1950.

So far this year 102 people have died on the roads, 15 more than at the same point in 2013, Assistant Commissioner Road Policing Dave Cliff said today.

The problem with this sort of story is how it omits the role of random variation — bad luck.  The Police are well aware that driving mistakes usually do not lead to crashes, and that the ones which do are substantially a matter of luck, because that’s key to their distracted driver campaign. As I wrote recently, their figures on the risks from distracted driving are taken from a large US study which grouped together a small number of actual crashes with a lot of incidents of risky driving that had no real consequence.

The importance of bad luck in turning bad driving into disaster means that the road toll will vary a lot. The margin of error around a count of 102 is about +/- 20, so it’s not clear we’re seeing more than misfortune in the change.  This is especially true because last year was the best on record, ever. We almost certainly had good luck last year, so the fact that it’s wearing off a bit doesn’t mean there has been a real change in driver behaviour.

It was a terrible, horrible, no good, very bad month on the roads, but some months are like that. Even in New Zealand.

This table is from a University of California alumni magazine

Jeff Leek argues at Simply Statistics that the big problem with Big Data is they, too, forgot statistics.

From Matthew Hankins, via a Cochrane Collaboration blog post, the first few items on an alphabetical list of ways to describe failure to meet a statistical significance threshold

a barely detectable statistically significant difference (p=0.073)
a borderline significant trend (p=0.09)
a certain trend toward significance (p=0.08)
a clear tendency to significance (p=0.052)
a clear trend (p<0.09)
a clear, strong trend (p=0.09)
a considerable trend toward significance (p=0.069)
a decreasing trend (p=0.09)
a definite trend (p=0.08)
a distinct trend toward significance (p=0.07)
a favorable trend (p=0.09)
a favourable statistical trend (p=0.09)
a little significant (p<0.1)
a margin at the edge of significance (p=0.0608)
a marginal trend (p=0.09)
a marginal trend toward significance (p=0.052)
a marked trend (p=0.07)
a mild trend (p<0.09)
…

Often there’s no need to have a threshold and people would be better off giving an interval estimate including the statistical uncertainty.

The defining characteristic of the (relatively rare) situations where a threshold is needed is that you either pass the threshold or you don’t. A marked trend towards a suggestion of positive evidence is not meeting the threshold.

From  Malaysian newspaper The Star, via Twitter, an infographic that gets the wrong details right

The designer went to substantial effort to make the area of each figure proportional to the number displayed (it says something about modern statistical computing that the my quickest way to check this was read the image file in R, use cluster analysis to find the figures, then tabulate).

However, it’s not remotely true that typical Malaysians weigh nearly four times as much as typical Cambodians. The number is the proportion above a certain BMI threshold, and that changes quite fast as mean weight increases.  Using 1971 US figures for the variability of BMI, you’d get this sort of range of proportion overweight with a 23% range in mean weight between the highest and lowest countries.

From Deadspin, an analysis of accuracy in 11 million tournament predictions (‘brackets’) for the US college basketball competition, and 53 predictions by experts

Stephen Pettigrew’s analysis shows the experts average more points than the general public (651681 vs 604.4). What he doesn’t point out explicitly is that picking the favourites, which corresponds to the big spike at 680 points, does rather better than the average expert.

The DimPost posted a new poll average and trend, which gives an opportunity to talk about some of the issues in interpretation (you should also listen to Sunday’s Mediawatch episode)

The basic chart looks like this

The scatter of points around the trend line shows the sampling uncertainty.  The fact that the blue dots are above the line and the black dots are below the line is important, and is one of the limitations of NZ polls.  At the last election, NZ First did better, and National did worse, than in the polling just before the election. The trend estimates basically assume that this discrepancy will keep going in the future.  The alternative, since we’ve basically got just one election to work with, is to assume it was just a one-off fluke and tells us nothing.

We can’t distinguish these options empirically just from the poll results, but we can think about various possible explanations, some of which could be disproved by additional evidence.  One possibility is that there was a spike in NZ First popularity at the expense of National right at the election, because of Winston Peters’s reaction to the teapot affair.  Another possibility is that landline telephone polls systematically undersample NZ First voters. Another is that people are less likely to tell the truth about being NZ First voters (perhaps because of media bias against Winston or something).  In the US there are so many elections and so many polls that it’s possible to estimate differences between elections and polls, separately for different polling companies, and see how fast they change over time. It’s harder here. (update: Danyl Mclauchlan points me to this useful post by Gavin White)

You can see some things about different polling companies. For example, in the graph below, the large red circles are the Herald-Digipoll results. These seem a bit more variable than the others (they do have a slightly smaller sample size) but they don’t seem biased relative to the other polls.  If you click on the image you’ll get the interactive version. This is the trend without bias correction, so the points scatter symmetrically around the trend lines but the trend misses the election result for National and NZ First.

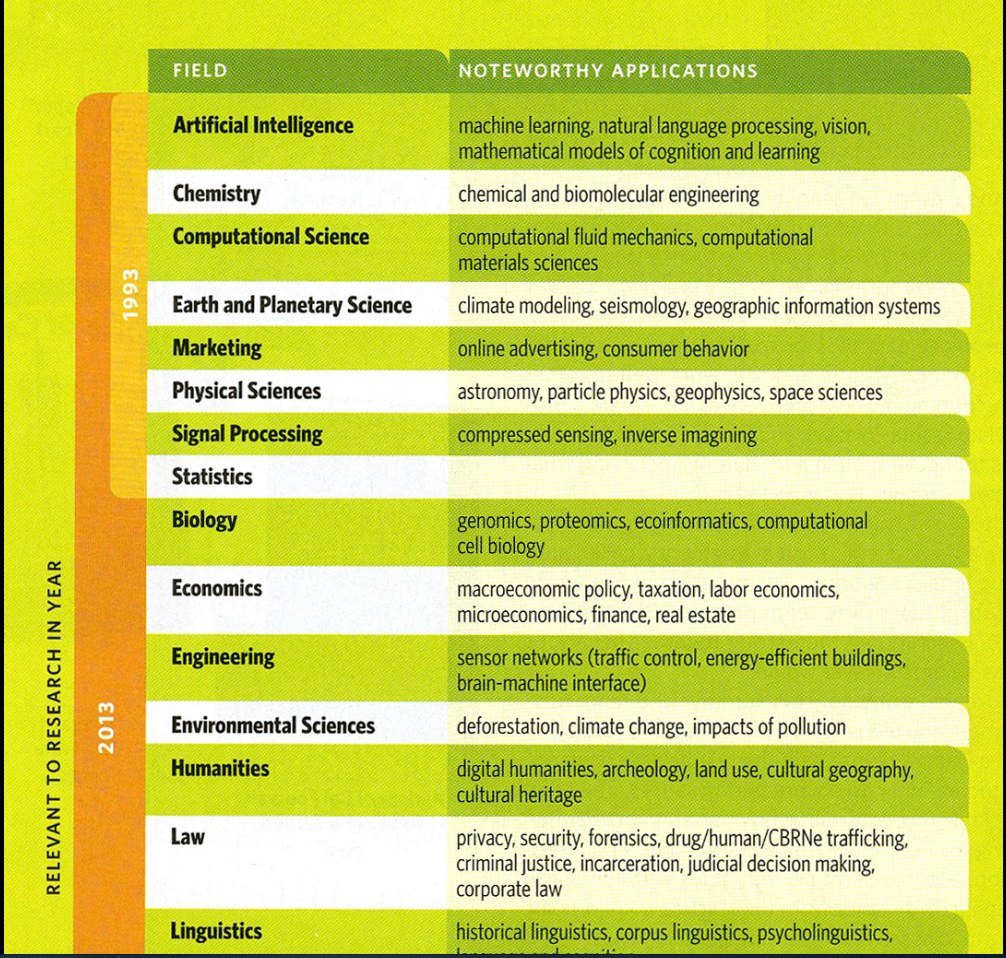
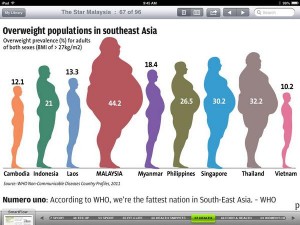
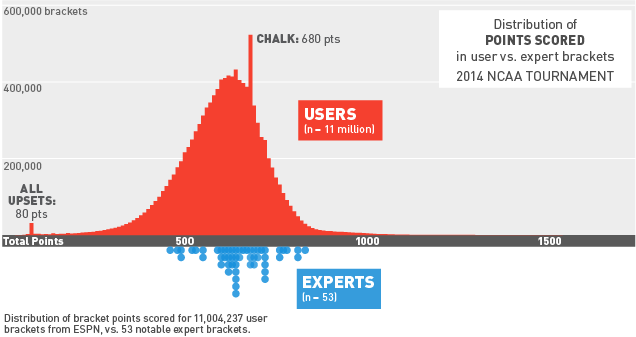
An XKCD classic

The mouseover text says “Also, all financial analysis. And, more directly, D&D.” 

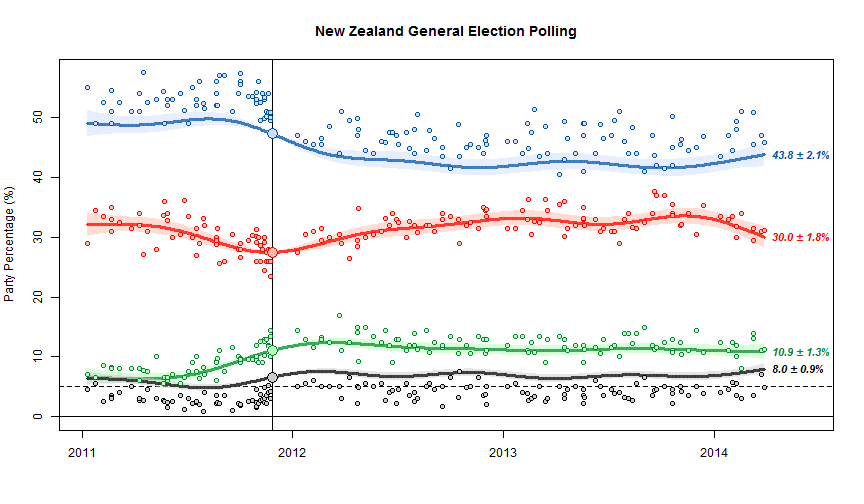
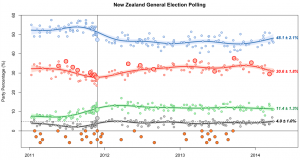
We’re getting to the point in the electoral cycle where opinion polls qualify as well. There will be lots of polls, and lots media and blog writing that tries to tell stories about the fluctuations from poll to poll that fit in with their biases or their need to sell advertising. So, as an aid to keeping calm and believing nothing, I thought a reminder about variability would be useful.

The standard NZ opinion poll has 750-1000 people. The ‘maximum margin of error’ is about 3.5% for 730 and about 3% for 1000. If the poll is of a different size, they will usually quote the maximum margin of error. If you have 20 polls, 19 of them should get the overall left:right division to within the maximum margin of error.

If you took 3.5% from the right-wing coalition and moved it to the left-wing coalition, or vice versa, you’d change the gap between them by 7% and get very different election results, so getting this level of precision 19 times out of 20 isn’t actually all that impressive unless you consider how much worse it could be. And in fact, polls likely do a bit worse than this: partly because voting preferences really do change, partly because people lie, and partly because random sampling is harder than it looks.

Often, news headlines are about changes in a poll, not about a single poll. The uncertainty in a change is  higher than in a single value, because one poll might have been too low and the next one too high.  To be precise, the uncertainty is 1.4 times higher for a change.  For a difference between two 750-person polls, the maximum margin of error is about 5%.

You might want a less-conservative margin than 19 out of 20. The `probable error’ is the error you’d expect half the time. For a 750-person poll the probable error is 1.3% for a single party and single poll,  2.6% for the difference between left and right in a single poll, and 1.9% for a difference between two polls for the same major party.

These are all for major parties.  At the 5% MMP threshold the margin of error is smaller: you can be pretty sure a party polling below 3.5% isn’t getting to the threshold and one polling about 6.5% is, but that’s about it.

If a party gets an electorate seat and you want to figure out if they are getting a second List seat, a national poll is not all that helpful. The data are too sparse, and the random sampling is less reliable because minor parties tend to have more concentrated support.   At 2% support the margin of error for a single poll is about 1% each way.

Single polls are not very useful, but multiple polls are much better, as the last US election showed. All the major pundits who used sensible averages of polls were more accurate than essentially everyone else.  That’s not to say experts opinion is useless, just that if you have to pick just one of statistical voodoo and gut instinct, statistics seems to work better.

In NZ there are several options. Peter Green does averages that get posted at Dim Post; his code is available. KiwiPollGuy does averages and also writes about the iPredict betting markets, and pundit.co.nz has a Poll of Polls. These won’t work quite as well as in the US, because the US has an insanely large number of polls and elections to calibrate them, but any sort of average is a big improvement over looking one poll at a time.

A final point: national polls tell you approximately nothing about single-electorate results. There’s just no point even looking at national polling results for ACT or United Future if you care about Epsom or Ohariu.

From Twitter, this morning (the graphs aren’t in the online story)

Does anybody else see the problem with this poll? Is this a representative sample? Good work @nzherald pic.twitter.com/63uwzbjZpZ

— Lennart Nout (@lennartnout) March 19, 2014

Now, the Herald-Digipoll is supposed to be a real survey, with samples that are more or less representative after weighting. There isn’t a margin of error reported, but the standard maximum margin of error would be  a little over 6%.

There are two aspects of the data that make it not look representative. Thr first is that only 31.3%, or 37% of those claiming to have voted, said they voted for Len Brown last time. He got 47.8% of the vote. That discrepancy is a bit larger than you’d expect just from bad luck; it’s the sort of thing you’d expect to see about 1 or 2 times in 1000 by chance.

More impressively, 85% of respondents claimed to have voted. Only 36% of those eligible in Auckland actually voted. The standard polling margin of error is ‘two sigma’, twice the standard deviation.  We’ve seen the physicists talk about ‘5 sigma’ or ‘7 sigma’ discrepancies as strong evidence for new phenomena, and the operations management people talk about ‘six sigma’ with the goal of essentially ruling out defects due to unmanaged variability.  When the population value is 36% and the observed value is 85%, that’s a 16 sigma discrepancy.

The text of the story says ‘Auckland voters’, not ‘Aucklanders’, so I checked to make sure it wasn’t just that 12.4% of the people voted in the election but didn’t vote for mayor. That explanation doesn’t seem to work either: only 2.5% of mayoral ballots were blank or informal. It doesn’t work if you assume the sample was people who voted in the last national election.  Digipoll are a respectable polling company, which is why I find it hard to believe there isn’t a simple explanation, but if so it isn’t in the Herald story. I’m a bit handicapped by the fact that the University of Texas internet system bizarrely decides to block the Digipoll website.

So, how could the poll be so badly wrong? It’s unlikely to just be due to bad sampling — you could do better with a random poll of half a dozen people. There’s got to be a fairly significant contribution from people whose recall of the 2013 election is not entirely accurate, or to put it more bluntly, some of the respondents were telling porkies.  Unfortunately, that makes it hard to tell if results for any of the other questions bear even the slightest relationship to the truth.

The cosmologists are excited today, and there is data visualisation all over my Twitter feed

RT @Resonaances: Parameter space of inflation as of today: pic.twitter.com/i45NLQX9DI Honestly didn’t think I was going to see > 0 for a while!

— Renee Hlozek (@reneehlozek) March 17, 2014

That’s a nice display of uncertainty at different levels of evidence, before (red) and after (blue) adding new data.  To get some idea of what is greater than zero and why they care, read the post by our upstairs neighbour Richard Easther (head of the Physics department)

Next week I’m visiting Iowa State University, one of the places where the discipline of statistics was invented. It’s going to be cold — the overnight minimum on Sunday is forecast at -25C — because another of the big winter storms is passing through.

The storms this year have been worse than usual. Minneapolis (where they know from cold) is already up to its sixth-highest number of days with the maximum below 0F (-18C, the temperature in your freezer). The Great Lakes have 88% ice cover, more than they have had for twenty years.

Looking at data from NOAA, this winter has been cold overall in the US, very slightly below the average for the past century or so.

However, that’s just the US. For the northern hemisphere as a whole, it’s been an unusually warm winter, well above historical temperatures

This has been your periodic reminder that weather news, for good reasons, gives you a very selective view of global temperature.