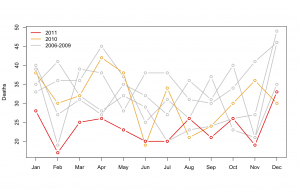
Road deaths down
A record low in road deaths last month has been accompanied by an unusually good Herald story. Andy Knackstedt from the Transport Agency is quoted as saying
“It’s too early to say what may or may not be responsible for the lower deaths over the course of one month.
“But we do know that over the long term, people are driving at speeds that are more appropriate to the conditions, that they’re looking to buy themselves and their families safer vehicles, that the engineers who design the roads are certainly making a big effort to make roads and roadsides more forgiving so if a crash does take place it doesn’t necessarily cost someone their life.”
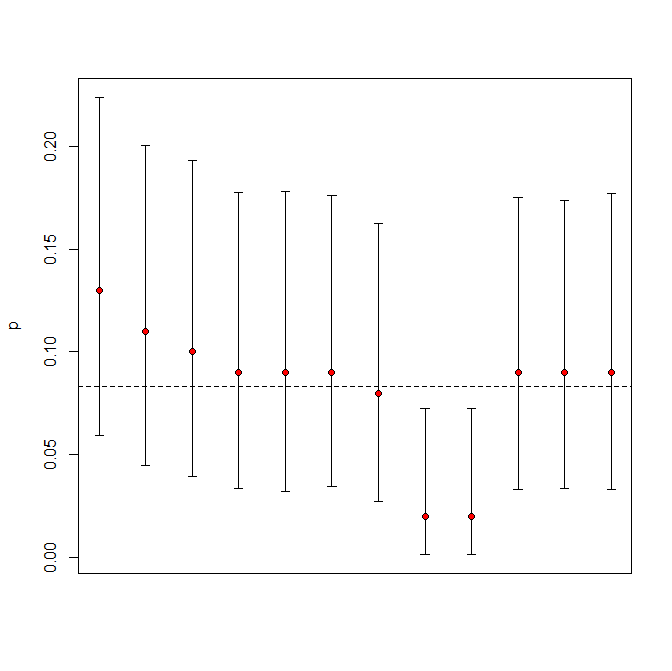
That’s a good summary. Luck certainly plays a role in the month-to-month variation, and these tend to be over-interpreted, but the recent trends in road deaths are real — much stronger than could result from random variation. We don’t know how much the state of the economy makes a difference, or more-careful driving following the rule changes, or many other possible explanations.
[Update: when I wrote this, I didn’t realise it was the top front-page story in the print edition, which is definitely going beyond the limits of the data]