Posts filed under Just look it up (283)

The New York Times has a well-deserved reputation for data journalism, but anyone can have a bad day.  There’s a piece by Steven Johnson on the non-extinction of the music industry (which I think makes some good points), but which the Future of Music Coalition doesn’t like at all. And they also have some good points.

In particular, Johnson says

“According to the OES, in 1999 there were nearly 53,000 Americans who considered their primary occupation to be that of a musician, a music director or a composer; in 2014 more than 60,000 people were employed writing, singing, or playing music. That’s a rise of 15 percent.”

He’s right. This is a graph (not that you really need one)

The Future of Music Coalition give the numbers for each year, and they’re interesting. Here’s a graph of the totals:

There isn’t a simple increase; there’s a weird two-humped pattern. Why?

Well, if you look at the two categories, “Music Directors and Composers” and “Musicians and Singers”, making up the total, it’s quite revealing

The larger category, “Musicians and Singers”, has been declining.  The smaller category, “Music Directors and Composers” was going up slowly, then had a dramatic three-year, straight-line increase, then decreased a bit.

Going  into the Technical Notes for the estimates (eg, 2009), we see

May 2009 estimates are based on responses from six semiannual panels collected over a 3-year period

That means the three-year increase of 5000 jobs/year is probably a one-off increase of 15,000 jobs. Either the number of “Music Directors and Composers” more than doubled in 2009, or more likely there was a change in definitions or sampling approach.  The Future of Music Coalition point out that Bureau of Labor Statistics FAQs say this is a problem (though they’ve got the wrong link: it’s here, question F.1)

Challenges in using OES data as a time series include changes in the occupational, industrial, and geographical classification systems

In particular, the 2008 statistics estimate only 390 of these people as being employed in primary and secondary schools; the 2009 estimate is 6000, and the 2011 estimate is 16880. A lot of primary and secondary school teachers got reclassified into this group; it wasn’t a real increase.

When the school teachers are kept out of  “Music Directors and Composers”, to get better comparability across years, the change is from 53000 in 1999 to 47000 in 2014. That’s not a 15% increase; it’s an 11% decrease.

Official statistics agencies try not to change their definitions, precisely because of this problem, but they do have to keep up with a changing world. In the other direction, I wrote about a failure to change definitions that led the US Census Bureau to report four times as many pre-schoolers were cared for by fathers vs mothers.

These ones are from the Seattle Times, since that’s where I was last week.

Amazon.com, like many other tech companies, had been persuaded to release figures on gender and ethnicity for its employees. On the original figures, Amazon looked  different from the other companies, but Amazon is unusual in being a shipping-things-around company as well as a tech company. Recently, they released separate figures for the ‘labourers and helpers’ vs the technical and managerial staff.  The pie chart shows how the breakdown makes a difference.

In contrast to Kirsty Johnson’s pie charts last week, where subtlety would have been wasted  given the data and the point she was making, here I think it’s more useful to have the context of the other companies and something that’s better numerically than a pie chart.

This is what the original figures looked like:

Here’s the same thing with the breakdown of Amazon employees into two groups:

When you compare the tech-company half of Amazon to other large tech companies, it blends in smoothly.

As a final point, “diversity” is really the wrong word here. The racial/ethnic diversity of the tech companies is pretty close to that of the US labour force, if you measure in any of the standard ways used in ecology or data mining, such as entropy or Simpson’s index.   The issue isn’t diversity but equal opportunity; the campaigners, led by Jesse Jackson, are clear on this point, but the tech companies and often the media prefer to talk about diversity.

From Kirsty Johnson, in the Herald, ethnicity in the highest and lowest decile schools in Auckland.

Statisticians don’t like pie charts because they are inefficient; they communicate numerical information less effectively than other forms, and don’t show subtle differences well.  Sometimes the differences are sufficiently unsubtle that a pie chart works.

It’s still usually not ideal to show just the two extreme ends of a spectrum, just as it’s usually a bad idea to show just two points in a time series. Here’s the full spectrum, with data from EducationCounts

[The Herald has shown the detailed school ethnicity data before in other contexts, eg the decile drift story and graphics from Nicholas Jones and Harkanwal Singh last year]

I’ve used counts rather than percentages to emphasise the variation in student numbers between deciles. The pattern of Māori and Pacific representation is clearly different in this graph: the numbers of Pacific students fall off dramatically as you move up the ranking, but the numbers of Māori students stabilise. There are almost half as many Māori students in decile 10 as in decile 1, but only a tenth as many Pacific students.

If you’re interested in school diversity, the percentages are the right format, but if you’re interested in social stratification, you probably want to know how students of different ethnicities are distributed across deciles, so the absolute numbers are relevant.

Two more visualisations:

Kieran Healy has graphs of the male:female ratio by age for each electorate. Here are the four with the highest female proportion,  rather dramatically starting in the late teen years.

Andrew Chen has a lovely interactive scatterplot of vote for each party against demographic characteristics. For example (via Harkanwal Singh),  number of votes for NZ First vs median age

• Ben Goldacre has a piece at Buzzfeed, which is nonetheless pretty calm and reasonable, talking about the need for data transparency in clinical trials

• The Alltrials campaign, which is trying to get regulatory reform to ensure all clinical trials are published, was joined this week by a group of pharmaceutical company investors.  This is only surprising until you think carefully: it’s like reinsurance companies and their interest in global warming — they’d rather the problems would go away, but there’s not profit in just ignoring them.

• The big potential success story of scanning the genome blindly is a gene called PCSK9: people with a broken version have low cholesterol. Drugs that disable PCSK9 lower cholesterol a lot, but have not (yet) been shown to prevent or postpone heart disease. They’re also roughly 100 times more expensive than the current drugs, and have to be injected. None the less, they will probably go on sale soon.
  A survey of a convenience sample of US cardiologists found that they were hoping to use the drugs in 40% of their patients who have already had a heart attack, and 25% of those who have not yet had one.

Stuff’s headline is “Beneficiaries increasingly failing drug tests, numbers show”.

The numbers are rates per week of people failing or refusing drug tests. The number was 1.8/week for the first 12 weeks of the policy and 2.6/week for the whole year 2014, and, yes, 2.6 is bigger than 1.8.  However, we don’t know how many tests were performed or demanded, so we don’t know how much of this might be an increase in testing.

In addition, if we don’t worry about the rate of testing and take the numbers at face value, the difference is well within what you’d expect from random variation, so while the numbers are higher it would be unwise to draw any policy conclusions from the difference.

On the other hand, the absolute numbers of failures are very low when compared to the estimates in the Treasury’s Regulatory Impact Statement.

MSD and MoH have estimated that once this policy is fully implemented, it may result in:

• 2,900 – 5,800 beneficiaries being sanctioned for a first failure over a 12 month period

• 1,000 – 1,900 beneficiaries being sanctioned for a second failure over a 12 month period

• 500 – 1,100 beneficiaries being sanctioned for a third failure over a 12 month period.

The numbers quoted by Stuff are 60 sanctions in total over eighteen months, and 134 test failures over twelve months.  The Minister is quoted as saying the low numbers show the program is working, but as she could have said the same thing about numbers that looked like the predictions, or numbers that were higher than the predictions, it’s also possible that being off by an order of magnitude or two is a sign of a problem.

From the Herald (squashed-trees version, via @economissive)

For comparison, a pie of those aged 65+ in NZ regardless of where they live, based on national population estimates:

Almost all the information in the pie is about population size; almost none is about where people live.

A pie chart isn’t a wonderful way to display any data, but it’s especially bad as a way to show relationships between variables. In this case, if you divide by the size of the population group, you find that the proportion in private dwellings is almost identical for 65-74 and 75-84, but about 20% lower for 85+.  That’s the real story in the data.

Brent Edwards on Radio NZ’s Checkpoint has done a good job of fact-checking claims about refugee numbers in New Zealand.  Amnesty NZ tweeted this summary table

If you want the original sources for the numbers, the Immigration Department Refugee Statistics page is here (and Google finds it easily).

The ‘Asylum’ numbers are in the Refugee and Protection Status Statistics Pack, the “Approved” column of the first table. The ‘Family reunification’ numbers are in the Refugee Family Support Category Statistics Pack in the ‘Residence Visas Granted’ section of the first table. The ‘Quota’ numbers are in the Refugee Quota Settlement Statistics Pack, in the right-hand margin of the first table.

Update: @DoingOurBitNZ pointed me to the appeals process, which admits about 50 more refugees per year: 53 in 2013/4; 57 in 2012/3; 63 in 2011/2; 27 in 2010/11.

This graphic and the accompanying story in the Herald produced a certain amount of skeptical discussion on Twitter today.

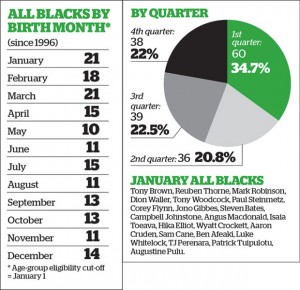
It looks a bit as though there is an effect of birth month, and the Herald backs this up with citations to Malcolm Gladwell on ice hockey.

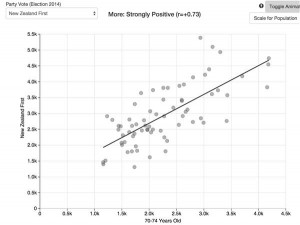
The first question is whether there is any real evidence of a pattern. There is, though it’s not overwhelming. If you did this for random sets of 173 people, about 1 in 80 times there would be 60 or more in the same quarter (and yes, I did use actual birth frequencies rather than just treating all quarters as equal). The story also looks at the Black Caps, where evidence is a lot weaker because the numbers are smaller.

On the other hand, we are comparing to a pre-existing hypothesis here. If you asked whether the data were a better fit to equal distribution over quarters or to Gladwell’s ice-hockey statistic of a majority in the first quarter, they are a much better fit to equal distribution over quarters.

The next step is to go slightly further than Gladwell, who is not (to put it mildly) a primary source. The fact that he says there is a study showing X is good evidence that there is a study showing X, but it isn’t terribly good evidence that X is true. His books are written to communicate an idea, not to provide balanced reporting or scientific reference.  The hockey analysis he quotes was the first study of the topic, not the last word.

It turns out that even for ice-hockey things are more complicated

Using publically available data of hockey players from 2000–2009, we find that the relative age effect, as described by Nolan and Howell (2010) and Gladwell (2008), is moderate for the average Canadian National Hockey League player and reverses when examining the most elite professional players (i.e. All-Star and Olympic Team rosters).

So, if you expect the ice-hockey phenomenon to show up in New Zealand, the ‘most elite professional players’, the All Blacks might be the wrong place to look.

On the other hand Rugby League in the UK does show very strong relative age effects even into the national teams — more like the 50% in first quarter that Gladwell quotes for ice hockey. Further evidence that things are more complicated comes from soccer. A paper (PDF) looking at junior and professional soccer found imbalances in date of birth, again getting weaker at higher levels. They also had an interesting natural experiment when the eligibility date changed in Australia, from January 1 to August 1.

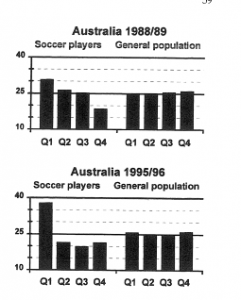
As the graph shows, the change in eligibility date was followed by a change in birth-date distribution, but not how you might expect. An August 1 cutoff saw a stronger first-quarter peak than the January 1 cutoff.

Overall, it really does seem to be true that relative age effects have an impact on junior sports participation, and possibly even high-level professional acheivement. You still might not expect the ‘majority born in the first quarter’ effect to translate from the NHL as a whole to the All Blacks, and the data suggest it doesn’t.

Rather more important, however, are relative age effects in education. After all, there’s a roughly 99.9% chance that your child isn’t going to be an All Black, but education is pretty much inevitable. There’s similar evidence that the school-age cutoff has an effect on educational attainment, which is weaker than the sports effects, but impacts a lot more people. In Britain, where the school cutoff is September 1:

Analysis shows that approximately 6% fewer August-born children reached the expected level of attainment in the 3 core subjects at GCSE (English, mathematics and science) relative to September-born children (August born girls 55%; boys 44%; September born girls 61% boys 50%)

In New Zealand, with a March 1 cutoff, you’d expect worse average school performance for kids born on the dates the Herald story is recommending.

As with future All Blacks, the real issue here isn’t when to conceive. The real issue is that the system isn’t working as well for some people. The All Blacks (or more likely the Blues) might play better if they weren’t missing key players born in the wrong month. The education system, at least in the UK, would work better if it taught all children as well as it teaches those born in autumn.  One of these matters.

The StatsNZ press release on marriages, civil unions, and divorces to December 2014 points out the dramatic fall in same-sex civil unions with 2014 being the first full year of marriage equality. Interestingly, if you look at the detailed data, opposite-sex civil unions have also fallen by about 50%, from a low but previously stable level.