Lotto, luck, and risk perception

There’s a big Lotto jackpot today, so it is my duty as a statistician to  write something about how people misunderstand probability. I don’t make the rules.

So, last week, I did a bogus poll on Twitter

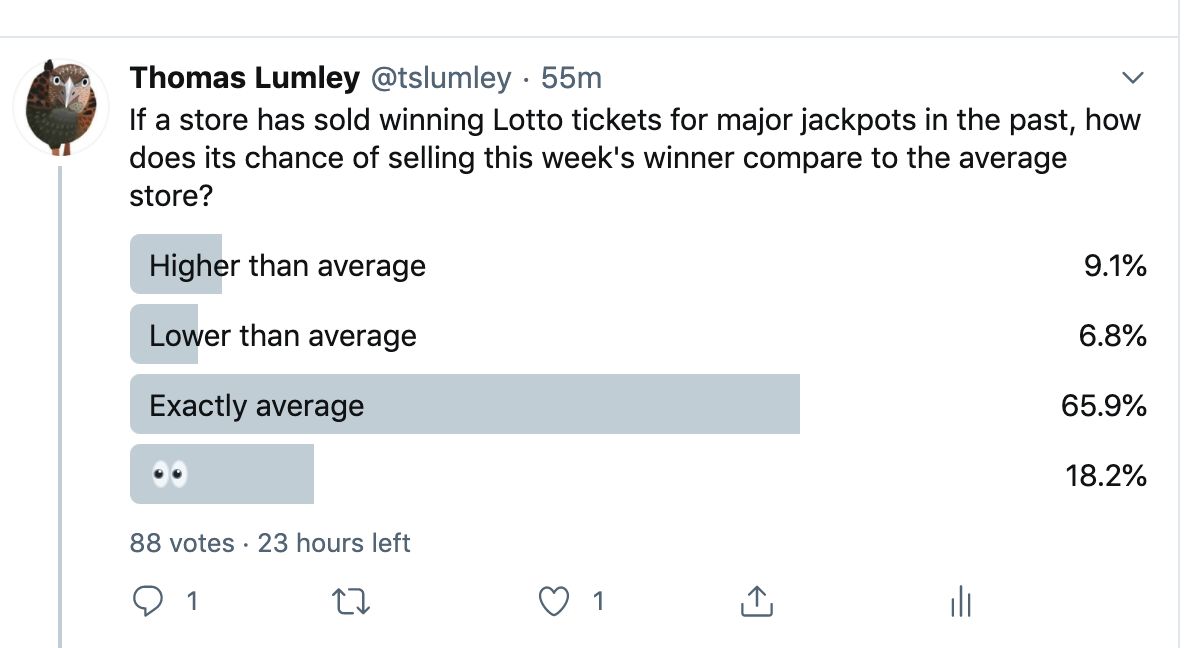
The results don’t tell you anything about any useful population,  because it was a bogus poll on Twitter, but it’s still interesting how many responses fell into the  trap.

Last week, we had headlines about ‘lucky’ stores to buy Lotto tickets.  Now, as you know, the probability that one of your chosen combinations wins does not depend at all on where you  bought the ticket, or how you chose the numbers. However, it is true that a shop which has sold winning tickets in the past is more likely to sell winning tickets in the future. Selling a winning ticket in the past is more likely for an outlet that sells lots of tickets, and an  outlet that sells lots of tickets is more  likely to sell  winning tickets in the future.  On top of that, it appears that people like to buy their tickets from outlets that have sold winning tickets in the past, which will increase the sales and therefore increase the number of future winners.  It doesn’t help the gamblers, but it does help the outlet.

In fact, saying it doesn’t help the  gamblers isn’t quite correct.   You’d hope, given the odds, that many people buying Lotto tickets were doing it primarily for entertainment (the cash return on tickets is negative, but that’s also true of beer and movies and rugby games and restaurant dinners).  Given that, anything that increases the entertainment value helps the gamblers,  and buying  from a ‘lucky’ store could count as a plus.

I also want to talk about a story in the Herald. It’s good on the  odds of winning and the impact of a ‘must win’ draw  — and quotes Dr Matt Parry, from Otago, which is generally a good indicator.  However, a separate part of the story says

Your chances of winning Powerball – one in 38 million – are less likely than you being struck by lightning – one in 280,000 – on your way to buy the ticket.

That seems not just wrong but incredibly wrong.   The story says “[m]ore than 1.9 million tickets were sold for the previous $50m must-be-won Powerball jackpot” (and that’s tickets, not lines), so at one in 280,000 we’d expect six or seven people to have been struck by lightning on their way to buy tickets.  According to this Radio NZ story, there were 13 ACC claims for lightning injury  in 3 years, and while that would leave out fatal injuries, the story also says a minority are fatal.  There’s no way you have a 1 in  280,000  chance of being struck by lightning on a routine shopping trip.

So where does this number come from? Well, the US also has a Powerball lottery, which has even lower odds of winning: one in  292 million. And there are news stories there with vaguely similar numbers.

The odds of grabbing the grand prize are 1 in 292.2 million, according to the game’s own assessment. To put this in context, your chances of being killed by a lightning strike are approximately 1 in 161,000. The odds of being killed in a shark attack are 1 in 3.7 million.

Even getting hit by a meteorite is more likely than winning the Powerball — 1 in 1.9 million.

The lightning-strike number looks to be a lifetime risk in the US, where lightning is more common than New Zealand, not the risk per shopping trip.

There are other problems with the numbers.  The 1 in 1.9 million for getting hit by a meteorite  is staggeringly wrong given that only one person in US history has been hit by a meteorite,  back in 1954.

How did the  1 in 1.9 million figure get past editing? Well, it probably wasn’t checked, but  there is a related number that’s arguably correct.  If you calculate the probability of dying due to a meteorite impact,  you have to consider the entire range of impacts from something the size of a golf  ball up to a significant asteroid.  The dinosaurs were wiped out (in part, probably) by an asteroid impact, 66 million years ago, so it would be reasonable to assume a risk in the ballpark of 1 in 100 million per year, giving a lifetime risk of experiencing the impact for an individual of one in a million or so.   Putting that together with expected  deaths from a major impact, it’s not unreasonable to get a 1 in two million risk for an individual  of dying because of an asteroid impact. On  the other hand, that’s not getting hit by a meteorite, and they shouldn’t be giving the number to two digits accuracy when even the order of magnitude must be uncertain.

So, if you’re in New Zealand and doing a careful risk assessment before buying a lottery ticket today, you probably don’t need to worry about lightning or low-flying rocks, but you should wear a mask. And if you’re in Auckland, maybe go to a local store or buy online.