Prediction is hard
From the Twitter account of the White House Council of Economic Advisors
From the Washington Post
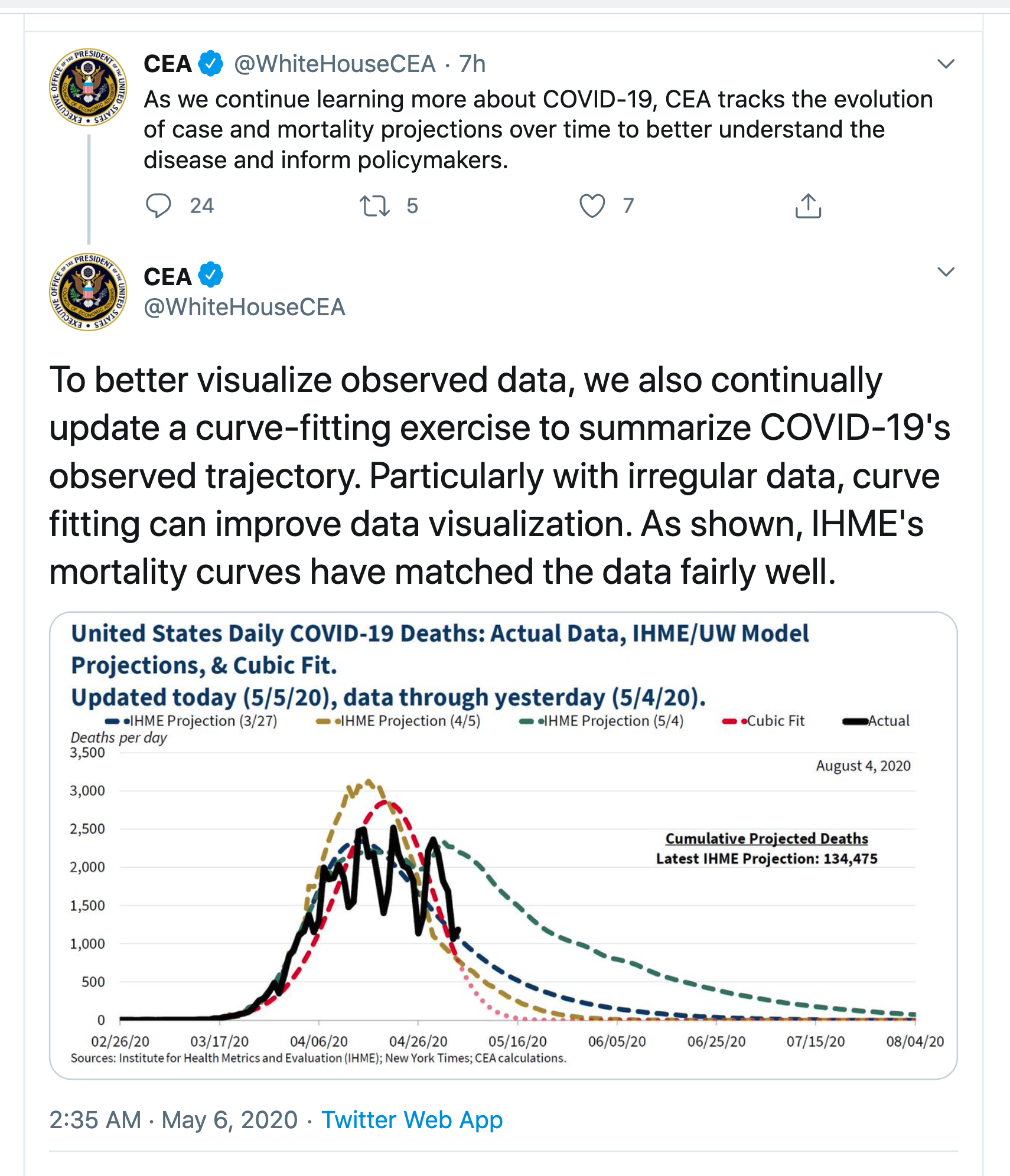
Even more optimistic than that, however, is the “cubic model” prepared by Trump adviser and economist Kevin Hassett. People with knowledge of that model say it shows deaths dropping precipitously in May — and essentially going to zero by May 15.
The red curve is, as the Post says, much more optimistic. None of them look that much like the data — they are all missing the weekly pattern of death reporting — but the IHME/UW model now predicts continuing deaths out until August. Even that is on the optimistic side: Trevor Bedford, a virologist at the University of Washington who has been heavily involved with the outbreak says he would expect a plateau lasting months rather than an immediate decline. Now, disagreement in predictions is nothing new and in itself isn’t that noteworthy. The problem is what the ‘cubic model’ means.
Prediction, as the Danish proverb says, is hard, because we don’t have any data from the future. We can divide predictive models into three broad classes
- Models based on understanding the actual process that’s causing the trends. The SIR models and their extensions, which we’ve seen a lot of in NZ, are based on a simplified but useful representation of how epidemics work. Weather forecasting works this way. So do predictions of populations for each NZ region into the future.
- Models based on simplifying and matching previous inputs. When Google can distinguish cat pictures from dog pictures, it’s because it has seen a bazillion of each and has worked out a summary of what cat pictures and dog pictures look like. It will compare your picture to those two summaries and see what matches best. Risk models for heart disease are like this: does your data look like the data of people who had heart attacks. Fraud risk models for banks, insurance companies, and the IRD work this way. It still helps a lot to understand about the process you’re modelling, so you know what sort of data to put in or leave out, and what sort of summaries to try to match.
- Models based on extrapolating previous inputs. In business and economics you often need predictions of the near future. These can be constructed by summarising existing recent trends and the variation around them, then assuming the trends and variation will stay roughly the same in the short term. Expertise in both statistics and in the process you’re predicting is useful, so that you know what sorts of trends there are and what information is available to model them. A key part of these time-series models is getting the uncertainty right, but even when you do a good job the predictions won’t work when the underlying trends change.
The SIR epidemiology models that you might have seen in the Herald are based on knowledge of how epidemics work. The IHME/UW models are at least based on knowledge of what epidemics look like. The cubic model isn’t.
The cubic fit is a model of the second type, based just on simplifying and matching the available data. It could be useful for smoothing the data — as the tweet says, “with irregular data, curve fitting can improve data visualization”. In particular, the weekly up-and-down pattern comes from limitations in the death reporting process, so filtering it out will give more insight into current trends.
The particular model that produces the red curve is extremely simple (Lucy D’Agostino McGowan duplicated it). If you write t for day of the year, so t starts at 1 for January 1, the model is
log(number of deaths + 0.5) = -0.0000393× t3 +0.00804× t2 -0.329×t – 0.865
What you can’t do with a smoothing/matching model like this is to extrapolate outside the data you have. If you have a model trained to distinguish cat and dog pictures and you give it a picture of a turkey, it is likely to be certain that the picture is a cat, or certain that the picture is a dog, but wrong either way. If you have a simple matching model where the predicted number of deaths depends only on the date, and the model matches data from dates in March and April, you can’t use it to predict deaths in June. The model has never heard of June. If it gets good predictions in June, that’s entirely an accident.
When you extrapolate the model forward in time, the right-hand side becomes very large and negative, so the predicted number of deaths is zero with extreme certainty. If you were to extrapolate backwards in time, the predicted number of deaths would explode to millions and billions during December. There’s obviously no rational basis for using the model to extrapolate backwards into December, but there isn’t much more for using it to extrapolate forward — nothing in the model fitting process cares about the direction of time.
The Chairman of the Council of Economic Advisers until the middle of last year was Dr Kevin Hassett (there’s no Chairman at the moment). He’s now a White House advisor, and the Washington Post attributes the cubic model to him. Hassett is famous for having written a book in 1999 predicting that the Dow Jones index would reach 36,000 in the next few years. It didn’t — though he was a bit unlucky in having his book appear just before the dot-com crash. Various unkind people on the internet have suggested a connection between these two predictive efforts. That’s actually completely unfair. Dow 36,000 was based on a model for how the stock and bond markets worked, in two parts: a theory that stocks were undervalued because of their relative riskiness, and a theory that the markets would realise this underpricing in the very near future. The predictions were wrong because the theory was wrong, but that’s at least the right way to try to make predictions. Extrapolating a polynomial isn’t.
Thomas Lumley (@tslumley) is Professor of Biostatistics at the University of Auckland. His research interests include semiparametric models, survey sampling, statistical computing, foundations of statistics, and whatever methodological problems his medical collaborators come up with. He also blogs at Biased and Inefficient See all posts by Thomas Lumley »
I happen to be writing a short section touching on predictive analytics within a longer work around the same time as I saw this post.
Your 3-way classification of predictive models makes intuitive sense to me. Is this a classification that is commonly used in the literature, or is there any canonical article that you’d recommend that delineates these?
Thanks in advance!
5 years ago
The two two-way classifications of process models vs empirical models and extrapolation vs interpolation are standard. I haven’t seen the three-way combination anywhere in particular
5 years ago
Thanks – much appreciated!
5 years ago
Hey there, been reading some very interesting articles you have written :)
Any chance you could crunch some numbers and evaluate the upcoming US election?
Regards
5 years ago
No, I’m leaving that for people like Nate Silver. Doing a good job at it would be a lot more work than I have time for.
5 years ago