Posts from April 2020 (5)

This isn’t precisely statistics, but Bloomberg Opinion may have set some kind of record for the density of easily checkable false statements in a single column that’s still making a basically sound argument.  Joe Nocera was arguing in favour of strict lockdown policy like the one in New Zealand.

Just looking at the tweets we have

1. New Zealanders aren’t allowed to drive except in emergencies and can only be out of the house for an hour a day, to get exercise or to buy essentials. This one-hour limit is enforced by the police. The one hour limit isn’t true, and so isn’t being enforced by police. The ‘only in emergencies’ is at best misleading: you can drive to buy essentials.
2. At the pharmacy, only one person is allowed in at a time, and clerks retrieve the goods so customers never touch anything until they return home. The wait to get in a grocery store is around an hour. If you don’t have a mask and gloves, you won’t get in. True as to pharmacies.  False as to the wait to get in a grocery store — which also contradicts the alleged one-hour limit.  False as to masks and gloves: the use of masks is encouraged by some groups but they are not required and users are only barely a majority, if that. Gloves aren’t even recommended.
3. In New Zealand…
   Every restaurant is closed.

   There’s no take-out.
   There are no deliveries.
   E-commerce has been halted. Food-processing companies still operate, but virtually every other form of blue-collar work is shut down. True on restaurant closures (until tomorrow).  It’s ambiguous whether ‘deliveries’ goes with the previous bullet or the following one, but e-commerce is certainly not halted. You can’t get prepared food delivered, but groceries, wine and spirits, some office equipment, and a range of other things are being delivered.  I have bought an office chair, because I’m working from home until at least the end of July.  The blue-collar work thing is true-ish — he may underestimate how much of NZ’s economy is in food production for export, but construction and forestry are shut down.  
4. Citizens are surviving financially with emergency checks from the government. Essential workers in New Zealand are truly essential. Although there are Covid-19 clusters — a church; a rest home; a wedding party — workplaces have largely been virus-free.  The Marist College cluster and the World Hereford Conference definitely count as ‘workplace’.  The government is primarily sending payments to businesses so they can keep employees or provide them sick leave, and to self-employed people, though there has obviously been an increase in the number of people getting unemployment benefits and applying for hardship grants. And, of course, we don’t use checks for all this.

It’s probably best to think of the column as ‘about New Zealand’ in the same way Gilbert and Sullivan’s Mikado is ‘about Japan’ — it’s really just a background setting to criticise the writer’s own country.

There have been three fairly large American seroprevalence studies recently.  These are studies that sample people from the community and test their blood for antibodies to the COViD-19 virus. Most people who have been infected, even if they recovered weeks ago, will have antibodies to the virus.  And people who have not been infected will not have antibodies to the COVID-19 virus, though the test isn’t perfect and will occasionally be confused by antibodies to something else.

The two studies in Los Angeles and in Santa Clara County (Silicon Valley) estimated that a few percent of people had been exposed to the virus. The New York study estimated far higher rates — in New York City itself, 21%.  The Californian studies have been widely criticised because of questions about the representativeness of the sample and the accuracy of the statistical calculations.  The New York study has had much less pushback.

One difference between the New York study and the others is that it’s not being pushed as a revolutionary change in our understanding of coronavirus, so people aren’t putting as much effort into looking at the details. Much more important, though, is that it is far easier to get a prevalence of 20% roughly right than to get a prevalence of 2-3% roughly right. If you make extraordinary claims based on a prevalence estimate of 2-3%, you need data and analysis of extraordinary quality (in a good way).  If your prevalence estimate of 20% is consistent with the other empirical data and models for coronavirus, it doesn’t need to stand on its own to the same extent.

Getting a good estimate of a prevalence of 2-3% is hard because the number of people who really have been exposed is going to be about the same as the number where the test gets confused and gives the wrong answer.  If you aren’t precisely certain of the accuracy of the test (and you’re not), the uncertainty in the true prevalence can easily be so large as to make the effort meaningless. On top of that, the quality of the sampling is critical:  even a little bit of over-volunteering by people who have been sick and want reassurance can drive up your estimate to be larger than the truth.  You can easily end up with an estimate saying the prevalence is much higher than most people expect, but only very weak evidence for that claim.

It looks as though the antibody test used in New York was less accurate than the one used in Santa Clara; the New York State lab that ran the testing says only that they are confident the rate of positive tests in truly unexposed people is less than 7%; their best-guess estimate will presumably be around 2-3%, in contrast with the best-guess estimate of 0.5% for test used in Santa Clara. But even, worst-case,  if 7% of tests were false positives, that still leaves 14% that were genuine. And since the test will miss some people who were truly exposed, the true prevalence will be higher than 14%. Suppose, for example, that the test picks up antibodies in 90% of people who really have been exposed. The 14% we’re seeing is only 90%80% of the truth, so the truth would be about 16%, and with a less-sensitive test, the truth would have to be higher.  So, even though the test is imperfect, somewhere between one in five and one in seven people tested had been exposed to the virus.  That’s a narrow enough range to be useful.  You still have to worry about sampling: it’s not clear whether sampling people trying to shop will give you an overestimate or an underestimate relative to the whole population, but the bias would have to be quite large to change the basic conclusions of the study.

The estimate for New York fits reasonably well with the estimate of roughly 0.1% for the proportion of the New York City population that have died because of the pandemic, and the orthodox estimate of around 1% for the proportion of infected people who will die of COViD.  These all have substantial uncertainty: I’ve talked about the prevalence estimate already. The infection fatality rate estimate is based on a mixture of data sets, all unrepresentative in different ways. And the excess mortality figure itself is fairly concrete, but it includes, eg, people who died because they didn’t try to get to hospital for heart attacks, and in the other direction, road deaths that didn’t happen.  It is still important that these three estimates fit together, and it correctly gives researchers more confidence in all the numbers.  The Californian studies imply only about 0.1% of infections are fatal, and that doesn’t fit the excess mortality data or the standard fatality rate estimate at all.

There’s an analogy that science is like a crossword¹. But it’s not a cryptic crossword, where correct answers are obvious once you see the trick. It’s the other sort of crossword, where potential answers to different clues support or contradict each other.  If the clue is “Controversial NZ party leader (7)” and using “Bridges” would force another clue to be a seven letter word ending in “b”, you might pencil in “Seymour” instead and await further evidence.

¹: Independently invented by multiple people including Susan Haack and Chad Orzel.

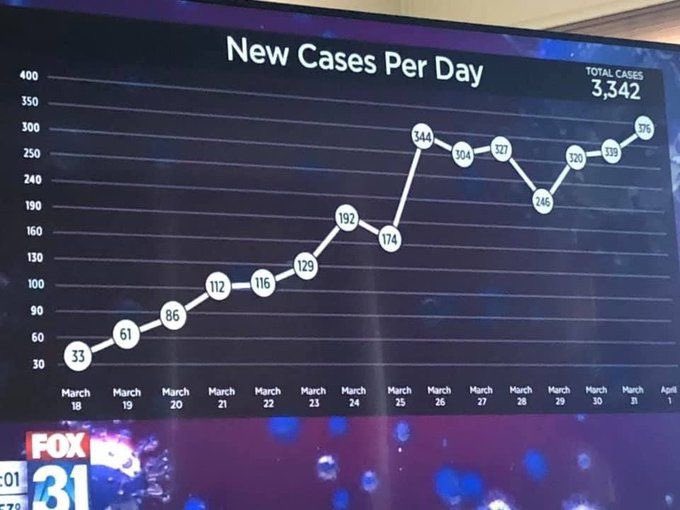
As promised, a second ‘prevalence’ post, this time on test accuracy.

In any medical diagnostic or screening setting, what we know is the number of positive and negative tests. What we want to know is the number of people with and without the condition.  It’s easy to slip into talking about these as if they’re the same, but they aren’t.

For the coronavirus, we have two basic sorts of test.  There  are ‘PCR’ tests, which is what everyone had been using.  And there are ‘antibody’ tests, which are new.

The PCR tests measure the presence of the virus. They transcribe the genetic material of the virus from RNA to DNA, and then use DNA copying enzymes to amplify it billions of times; the ‘polymerase chain reaction’.  After amplification, there’s enough of the genetic sequence that fluorescent dyes attached to it or to the input materials can produce measurable light.

The copying looks for a unique, fairly short, genetic sequence that’s present in the new coronavirus, but not in the SARS or MERS viruses, or the four coronaviruses that cause common colds (in fact, usually more than one genetic sequence, plus a ‘positive control’ that makes sure the process is working, plus a ‘negative control’ that doesn’t have any RNA). Because of the fidelity of DNA replication, the technical ‘assay error’ of the PCR test is so close to zero as makes no difference: a few copies of the virus are enough for a positive result, and it’s almost impossible to get a positive result without any virus.

Unfortunately, the real-world diagnostic error isn’t quite that good.  The false positive rate is still basically zero, given good lab practice; you can’t get a positive test without viral RNA from some source.  The false negative rate can be appreciable, because the test doesn’t ask if there’s virus somewhere in your system; it asks if there’s virus on the swab.   In early COViD-19 disease, the best way to grab some virus is to stick a swab almost far enough up your nose to do brain surgery, and twist it around a bit.   More often than not, this will pick up some virus. But if you get tested too early, there might not be enough virus, and if you get tested too late the infection might have relocated to your chest.

So how good is the PCR test in practice? Well, we don’t know for sure.  It’s the best test we have, so there isn’t a ‘true answer’ to compare it to.  However, a study that looked at tests using multiple ways of extracting a sample, suggest the sensitivity of the test is 65%: if you have early-stage COViD-19, you’ve got about a two in three chance of testing positive.  There’s a lot of uncertainty around the exact value; fortunately the exact value doesn’t matter all that much.

Antibody tests are new for coronavirus, but are familiar in other settings.  Older HIV tests looked for antibodies to the virus, as do the initial tests for Hepatitis C (which are followed up by PCR).  These antibody tests rely on the highly selective binding of antibodies to the antigens they detect. Because antibody tests detect your body’s reaction to the virus, a positive reaction takes time — at least a few days, maybe a week — and it stays around at least a short time after you recover.  Antibody tests are amazingly accurate, but not quite as amazingly accurate as PCR. Everyone has exactly the same identifying genetic tags in their virus, but everyone makes slightly different antibodies to the virus.  An antibody test is trying to pick up everyone’s diverse antibodies to the new coronavirus, but not pick up anyone’s antibodies to the nearly infinite diversity of other antigens in the world, including other coronaviruses. At any point in time, there’s a tradeoff: a test that picks up coronavirus antibodies more sensitively will also pick up more other things, and one that avoids reacting to other things will miss more coronavirus infections.

As I said above, the exact value of the false negative positive rate doesn’t matter that much when you’re estimating population prevalence.  The false positive negative rate matters a lot.  Suppose you have an antibody test with a false positive rate of 5%. For every 100 truly-negative people you test, there will be an average of 5 positive tests; for every 1000 people, 50 positive tests.  In New Zealand, we’re sure the population prevalence is less than 1%, and I would expect it to be less than 0.1%.  If you gave this test to 1000 people, there would be an average 50 positive results and maybe one or two true positives. It is very much an average, so if you got 53 positive tests you would have no idea whether that was five true positives or three or none at all.  Even if the false positive rate were as low as 0.5%, you’d expect more false positives than true positives in New Zealand. And it’s worse than that: the error rates aren’t known accurately yet, so even if the manufacturer’s estimate was 0.5% false positives, it could easily be 1% or maybe even 2%.

There’s a new study out of Stanford (preprint) that tested 3330 people and found 50 positives. A helpful StatsChat reader posted a link to a review of this study. What I’m writing here agrees pretty closely with that review.

A rate of 50 positives out of 3330 healthy people is high: if true, it would imply COViD-19 was much more common and therefore much less serious than we thought. The researchers used a test that had given 2 positive results out of 401 samples known to be negative (because they were taken before the pandemic started).  If the false positive rate was exactly 2/401 , you’d get 0.005×3330 false positives on average, or only about 17, leaving 33 true positives.  But 2/401 is an estimate, with uncertainty.  If we assume the known samples were otherwise perfectly representative, what we can be confident of with 2 positives out of 401 is only that the false positive rate is no greater than 1.5%. But 1.5% of 3330 is 50, so a false positive rate of 1.5% is already enough to explain the results! We don’t even have to worry if, say, the researchers chose this test from a range of competitors because it had the best supporting evidence and thereby introduced a bit of bias.

On top of that, the 3330 people were tested because they responded to Facebook ads.  Because infection is rare, you don’t need to assume much self-selection of respondents to bias the prevalence estimate upwards.  You might be surprised to see me say this, because yesterday I thought voluntary supermarket surveys were a pretty good idea. They are, but they will still have bias, which could be upwards or downwards. We wouldn’t use the results of a test in a few supermarkets to overturn the other evidence about disease severity; we want to use them to start finding undetected cases — any undetected cases.

Counting rare things is hard, and false positives are overwhelmingly more important than false negatives, which is currently a problem for antibody tests.  PCR tests based on a swab are unpleasant for the person being tested and risky for the person holding the swab, but they are the best we have now. There might be other ways to use antibody tests, for example if true infections cluster more strongly within household than false positives, or if two tests with different characteristics can be combined, or if more accurate ones become available. But it’s not easy. 

One of the known unknowns about the NZ coronavirus epidemic is the number of cases we have not detected.  There will have been a mixture of people who didn’t get any symptoms, people who are going to show symptoms but haven’t yet, people who got moderately sick but didn’t get tested, and people whose deaths were attributed to some pre-existing condition without testing.

For the decision to loosen restrictions, we care mostly about people who are currently infected, who aren’t (currently) sick enough to get testing, and who aren’t known contacts of previous cases.  What can we say about this number — the ‘community prevalence’ of undetected coronavirus infection in New Zealand?

One upper bound is that we’re currently seeing about 1% positive tests in people who either have symptoms or are close contacts of cases.  The prevalence in close contacts of cases must be higher than in the general population — this is an infectious disease — so we can be fairly confident the population prevalence is less than 1%.

Are there any other constraints? Well, infection isn’t a static process.  If you have coronavirus in 1% of Kiwis, they will pass it on to other people and they themselves will recover.  At the moment, under level 4, the epidemic modellers at Te Pūnaha Matatini are estimating a reproduction number of about 0.5, so 50,000 cases will infect half that many new people.  Now, if we’re missing nearly all the cases, the modelling might not be all that accurate, but there would have to be tens of thousands of new infections.  And at least a few percent of those new cases will be sick enough to need medical treatment.  We would quickly notice that many people showing up to hospitals with (by assumption) no known contacts.  It isn’t happening. Personally, I have a hard time believing in a prevalence as high as 0.2%, which would mean we’re missing over 80% of cases.

The other constraint would come from testing of healthy people, which is why the government has started doing that.  If you wanted an accurate estimate for the population as a whole, you’d need some sort of random population sample, but in the short time it makes more sense to take a sensibly-constructed random sample of supermarkets and then test their customers and employees — if there’s major undetected spread, supermarkets are one of the likely places for  it to happen, and they’re also a convenient place to find people who are already leaving home, so you can test them without barging into their bubbles.  So, we aren’t getting a true population prevalence estimate, but we are getting an estimate of something a bit like it but probably higher.

How many do we need to test? It depends on how sure you want to be. If we sample 10,000 people and 4 are positive, we could estimate^* prevalence at 4/10,000, or 0.04%.  But what if no-one is positive? The best estimate clearly isn’t zero!

The question gets more extreme with smaller sample sizes: if we sample 350 people (as was done at the Queenstown PakNSave) and find no cases, what can we say about the prevalence?  The classical answer, a valuable trick for hallway statistical consulting, is that if the true rate is 3/N or higher, the chance of seeing no cases in N tests is less than 5%. So, if we see no cases in 350 people, we can be pretty sure the prevalence was less than 3/350, or about 1%.  Since we were already pretty sure the prevalence was way less than 1%, that hasn’t got us much further forward.  We’re eventually going to want thousands, or tens of thousands, of tests. The Queenstown testing was only a start.

After that introduction, you’ll understand my reaction when Radio NZ’s Checkpoint said there had been a positive test in the Queenstown supermarket, with only two-thirds of the samples run through the lab.   Fortunately, it turns out there had been a misunderstanding and there has not yet been a positive result from this community testing.  If the true rate is 0.1% there’s a good chance we’ll see a community-positive test soon; if it’s 0.01%, not for a while.  And if we’re really at the level of eliminating community transmission, even longer.

Update: Statistical uncertainty in the other direction also matters.  If the true prevalence is p and you test N people, you get pN positive tests on average, but your chance of getting no positive tests is e^-pN. So, if you test 350 people and the true prevalence is 0.1%, your chance of getting no positive tests is about 70% and your chance of at least one positive is 30%.  And a positive test in Queenstown would have been surprising, but shouldn’t have been a complete shock. Two positive tests should be a shock.

* There’s another complication, for another post, in that the test isn’t perfect. The estimate would actually be more like 0.05% or 0.06%.

A graph from Fox31 news, via various people on Twitter.

Look at the y-axis: the divisions vary from 10 to 50!

The natural suspicion is that the y-axis has been fiddled to make the graph look more linear — to ‘flatten the curve’.

So, I tried drawing it right, to show the actual trend. It looks

…. pretty much the same, actually.

So, on the one hand, no real distortion of the data.  But on the other hand, why bother?