Road toll still down.

The police are urging people to drive carefully this weekend, which is a good idea as always.  They are also reducing their speeding threshold to 4km/h over the limit, saying that this “had made a big difference during previous holiday periods”, and that they want to “avoid a repeat of last year’s carnage, in which seven people were killed on the roads”. The lower speed tolerance was bought in for the Queens Birthday weekend 2010, which was before last year, so at least for Labour day it doesn’t seem to have made much difference.

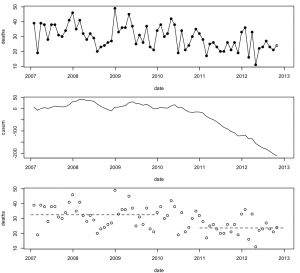
It’s always hard to interpret figures for a single weekend (or even a single month) because of random variation.  Here’s the data for the past six years (from, and)

The top panel shows monthly deaths, with October 2012 as an open circle because the number there is an extrapolation by doubling the deaths for Oct 1-15.  There’s a lot of month-to-month variability, and the trend isn’t that obvious.

The second panel shows cumulative sums of deaths minus the average number for 2007-2009, a chart used in industrial process monitoring. The curve is basically flat until mid-2010, and then starts a steady decline, suggesting that a new, lower, average started in mid-2010 and has been pretty stable since.  The current value of the curve, at -200, means that 200 people are still alive who would have died on the roads if the rates were still at the 2007-2009 levels.

The third panel shows the monthly deaths again, with horizontal lines at the average for 2007-2009 and 2011-12, confirming that there was a decrease to a new, relatively stable level. The decrease doesn’t just happen in months with holiday weekends, so it’s unlikely to just be the tightened speeding tolerance causing it. It would be good to know what is responsible, and there are plenty of theories, but not much evidence.