There’s nothing like a good joke.

Q:  Have you started eating more chocolate yet?

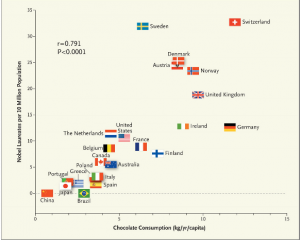
A: I assume this is about the New England Journal paper.

Q: Of course.  You could increase your chance of a Nobel Prize

A: There are several excellent reasons why I am not going to get a Nobel Prize, but in any case I don’t have to eat the chocolate: anyone in Australia or New Zealand would do just as well. You can have my share.

Q:  What do you mean?

A: The article didn’t look at chocolate consumption by Nobel Prize winners, it looked at chocolate consumption in countries named in the official biographical information about Nobel Prize winners.  This typically includes where they were born and where they worked when they did the prize-winning research, and in some cases yet another country where they currently work.

Q: Does the article admit this?

A: In part.  The author admits that this is just per-capita data, not individual data.  Because he just got the Nobel Prize data from Wikipedia, rather than from the primary source, he doesn’t seem to have noticed that multiple countries per recipient are counted.

Q: Would the New England Journal of Medicine usually accept Wikipedia as a data source when the primary data are easily available?

A: No.

Q: What about the chocolate data?

A: The author doesn’t say whether the chocolate consumption measures weight as consumed (ie, including milk and sugar) or weight of actual chocolate content. That’s especially sloppy since he goes on and on about flavanols. Also, the Nobel Prize data is for 1901-2011 and the chocolate data is mostly just from 2010 or 2011: chocolate consumption in many countries has changed over the past century.

Q: Do you want to say something about correlation and causation now?

A: No, that’s what you say when you don’t know what causes spurious correlations.

Q: So what did cause this correlation?

A: There are at least two likely contributions.  The first is just that wealthy countries tend to have more chocolate consumption and more Nobel Prizes.  Chocolate and research are expensive.  The second is more interesting: it’s the same reason that storks per capita and birth rates are correlated.

Q: Storks bring chocolate as well as babies?

A: Not quite.  Birth rates and storks per capita tend to be correlated because they are both multiples of the reciprocal of population size.   Jerzy Neyman pointed this out in the prehistory of statistics, and Richard Kronmal brought it up again in 1993.  More recently, someone has done the computation with real data (p=0.008). Imperfect standardisation will induce correlation, and since Nobel Prizes almost certainly don’t depend linearly on population, the correction is bound to be imperfect.

Q: Why did the New England Journal publish this article?

A: It wasn’t published as a research article; it was in their ‘Occasional Notes’ series, which the journal describes as “accounts of personal experiences or descriptions of material from outside the usual areas of medical research and analysis.”

Q: Isn’t it good that stuffy medical journals do this sort of thing occasionally? There’s nothing like a good joke

A: Well, you might hope they would do it better, like the BMJ does.  This is nothing like a good joke.