Posts from June 2012 (33)

As you will have heard, the UN says that Kiwis smoke more pot than anyone else.  The figure quoted, eg, by the Herald is 9.1%-14.6% (they don’t say what the range means).  It’s useful to look at the actual survey data, the NZ Alcohol and Drug Use survey, which is conveniently available online.

The proportion of New Zealanders who used cannabis at least weekly in the past year is about 5.6%, and the proportion who used it more than 1-2 times/week is 3.8%.  For tobacco, the corresponding figure for more than 1-2 times per week is about 20% and for alcohol, 26%.

You can find statistics broken down by age, sex, ethnicity, frequency of use, and indicators of dependency (yes, people do get addicted to cannabis, just like to other drugs).

The political/social science/etc blog Crooked Timber is having a seminar on Open Data, which is highly recommended.  In one of the posts, Steven Berlin Johnson writes about the mid-19th century efforts of William Farr to publish more information on causes of death, information later used by John Snow in attributing cholera to contaminated water.

He concludes:

Yes, information abundance meant that the newspapers lost their local advertising monopolies to Craigslist and Groupon, but it also means that the crucial data they used to have to unearth by hanging around City Hall for months is now available to anyone with a Web browser or an API key. We may well have fewer investigative journalists on the payroll of newspapers, but if we play our Open Data cards right, we might well end up with more investigations.

[Update: these are now all collected in a post and PDF and epub]

The Herald has a good report of research to be published in Science tomorrow, studying earthquakes on the Alpine fault.  By looking at a river site where quakes disrupted water flow, interrupting peat deposition with a layer of sediment, the researchers could get a history of large quakes going back 8000 years. They don’t know exactly how big any of the quakes were, but they were big enough to rupture the surface and affect water flow, so at the least they would mess up roads and bridges, and disrupt tourism.

Based on this 8000-year history, it seems that the Alpine fault is relatively regular in how often it has earthquakes: more so than the San Andreas Fault in California, for example.  Since the fault has major earthquakes about every 330 years, and the most recent one was 295 years ago, it’s likely to go off soon.  Of course, ‘soon’ here doesn’t mean “before the Super 15 final”; the time scales are a bit longer than that.

We can look at some graphs to get a rough idea of the risk over different time scales.  I’m going to roughly approximate the distribution of the times between earthquakes by a log-normal distribution, that is, the logarithm of the times has a Normal distribution.

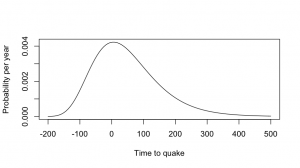This is a simple and reasonable model for time intervals, and it also has the virtue of giving the same answers that the researchers gave to the press.  Using the estimates of mean and variation in the paper, the distribution of times to the next big quake looks like the first graph.  The quake is relatively predictable, but “relatively” in this sense means “give or take a century”.

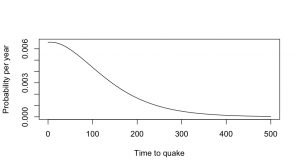Now, by definition, the next big quake hasn’t happened yet, so we can throw away the part of this distribution that’s less than zero, and rescale the distribution so it still adds up to 1, getting the second graph.  The chance of a big quake is a bit less than 1% per year — not very high, but certainly worth doing something about.  For comparison, it’s about 2-3 times the risk per year of being diagnosed with breast cancer for middle-aged women.

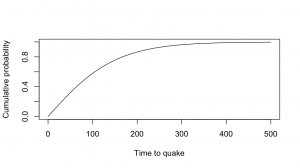
The Herald article (and the press release) quote a 30% chance over 50 years, which matches this lognormal model.  At 80 years there’s a roughly 50:50 chance, and if we wait long enough the quake has to happen eventually.

The risk of a major quake in any given year isn’t all that high, but the problem isn’t going away and the quake is going to make a serious mess when it happens.

[Update: Stuff also has an article. They quote me  (via the Science Media Centre) , but I’m just describing one of the graphs in the paper: Figure 3B, if you want to go and check that I can do simple arithmetic]

Team Ratings for Round 17

Here are the team ratings prior to Round 17, along with the ratings at the start of the season. I have created a brief description of the method I use for predicting rugby games. Go to my Department home page to see this.

Performance So Far

So far there have been 117 matches played, 70 of which were correctly predicted, a success rate of 59.83%.

Here are the predictions for last week’s games.

Predictions for Round 17

Here are the predictions for Round 17

Team Ratings for Week 19

Here are the team ratings prior to Week 19, along with the ratings at the start of the season. I have created a brief description of the method I use for predicting rugby games. Go to my Department home page to see this.

Performance So Far

So far there have been 100 matches played, 69 of which were correctly predicted, a success rate of 69%.

Here are the predictions for last week’s games.

Predictions for Week 19

Here are the predictions for Week 19. The prediction is my estimated points difference with a positive margin being a win to the home team, and a negative margin a win to the away team.

Each week, we would like to invite readers of Stats Chat to submit nominations for our Stat of the Week competition and be in with the chance to win an iTunes voucher.

Here’s how it works:

• Anyone may add a comment on this post to nominate their Stat of the Week candidate before midday Friday June 29 2012.
• Statistics can be bad, exemplary or fascinating.
• The statistic must be in the NZ media during the period of June 23-29 2012 inclusive.
• Quote the statistic, when and where it was published and tell us why it should be our Stat of the Week.

Next Monday at midday we’ll announce the winner of this week’s Stat of the Week competition, and start a new one.
(more…)

If you’d like to comment on or debate any of this week’s Stat of the Week nominations, please do so below!

Team Ratings for Round 16

Here are the team ratings prior to Round 16, along with the ratings at the start of the season. I have created a brief description of the method I use for predicting rugby games. Go to my Department home page to see this.

Performance So Far

So far there have been 110 matches played, 66 of which were correctly predicted, a success rate of 60%.

Here are the predictions for last week’s games.

Predictions for Round 16

Here are the predictions for Round 16

A fairly large fraction of the spam advertising the chance to capitalise on stolen riches is sent by Nigerian criminals.  What should be more surprising is the fact that a lot of the spam actually says it’s from Nigeria (or other West African nations).  Since everyone knows about Nigerian scams, why don’t the spammers claim to be from somewhere else? It’s not as if they have an aversion to lying about other things.

A new paper from Cormac Herley at Microsoft Research has a statistically-interesting explanation:  the largest cost in spam operations is in dealing with the people who respond to the first email.  Some of these people later realise what’s going on and drop out without paying; from the spammer’s point of view these are false positives — they cost time and money to handle, but don’t end up paying off.   A spammer ideally wants only to engage with the most gullible potential victims; the fact that ‘Nigeria’ will spark suspicions in many people is actually a feature, not a bug.

League tables work well in sports.  The way the competition is defined means that ‘games won’ really is the dominant factor in ordering teams,  it matters who is at the top, and people don’t try to use the table for inappropriate purposes such as deciding which team to support.  For schools and hospitals, not so much.

The main problems with league tables for schools (as proposed in NZ) or hospitals (as implemented in the UK) are, first, that a ranking requires you to choose a way of collapsing multidimensional information into a rank, and second, that there is usually massive uncertainty in the ranking, which is hard to convey.   There doesn’t have to be one school in NZ that is better than all the others, but there does have to be one school at the top of the table.  None of this is new: we have looked at the problems of collapsing multidimensional information before, with rankings of US law schools, and the uncertainty problem with rates of bowel cancer across UK local government areas.

This isn’t to say that school performance data shouldn’t be used.  Reporting back to schools how they are doing, and how it compares to other similar schools, is valuable.  My first professional software development project (for my mother) was writing a program (in BASIC, driving an Epson dot-matrix printer) to automate the reports to hospitals from the Victorian Perinatal Data Collection Unit.  The idea was to give each hospital the statewide box plots of risk factors (teenagers, no ante-natal care), adverse outcomes (deaths, preterm births, malformations), and interventions (induction of labor, caesarean section), with their own data highlighted by a line.   Many of the adverse outcomes were not the hospital’s fault, and many of the interventions could be either positive or negative depending on the circumstances, so collapsing to a single ‘hospital quality’ score would be silly, but it was still useful for hospitals to know how they compare.  In that case the data was sent only to the hospital, but for school data there’s a good argument for making it public.

While it’s easy to see why teachers might be suspicious of the government’s intentions, the rationale given by John Key for exploring some form of official league table is sensible.  It’s definitely better not to have a simple ranking, and it might arguably be better not to have a set of official comparative reports, but the data are available under the Official Information Act.  The media may currently be shocked and appalled at the idea of league tables, but does anyone really believe this would stop a plague of incomplete, badly-analyzed, sensationally-reported exposés of “New Zealand’s Worst Schools!!”?  It would be much better for the Department of Education to produce useful summaries, preferably not including a league-table ranking, as a prophylactic measure.