Cancer isn’t just bad luck
From Stuff
Bad luck is responsible for two-thirds of adult cancer while the remaining cases are due to environmental risk factors and inherited genes, researchers from the Johns Hopkins Kimmel Cancer Center found.
The idea is that some, perhaps many, cancers come from simple copying errors in DNA replication. Although DNA copying and editing is impressively accurate, there’s about one error for every three cell divisions, even when nothing is wrong. Since the DNA error rate is basically constant, but other risk factors will be different for different cancers, it should be possible to separate them out.
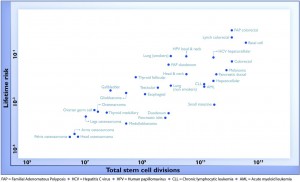
For a change, this actually is important research, but it has still been oversold, for two reasons. Here’s the graph from the paper showing the ‘2/3’ figure: the correlation in this graph is about 0.8, so the proportion of variation explained is the square of that, about two-thirds. (click to embiggen)
There are two things to notice about this graph. First, there are labels such as “Lung (smokers)” and “Lung (non-smokers)”, so it’s not as simple as ‘bad luck’. Some risk factors have been taken into account. It’s not obvious whether this makes the correlation higher or lower.
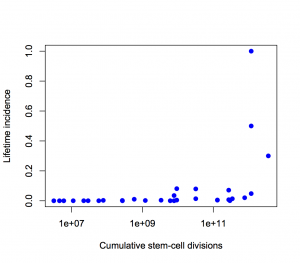
Second, the y-axis is on a log scale, so the straight line fit isn’t to cancer incidence and the proportion of variation explained isn’t a proportion of cancer risk. Using a log scale for incidence is absolutely right when showing the biological relationship, but you can’t read proportions of incidence explained off that graph. This is what the graph looks like when the y-axis is incidence, either with the x-axis still on a logarithmic scale
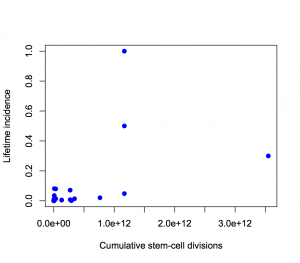
or with neither axis on a logarithmic scale
The proportion of variation explained is 18% and 28% respectively.
It’s ok to transform the x-axis as much as we like, so I looked at a square root transformation on the x-axis (based on the slope of the log-log graph). This gets the proportion of incidence explained up to about one third. Not two-thirds.
Using the log scale gives a lot more weight to the very rare cancers in the lower left corner, which turn out not to have important modifiable risk factors. Using an untransformed y-axis gives equal weight to all cancers, which is what you want from a medical or public health point of view.
Except, even that isn’t quite right. If you look at my two graphs it’s clear that the correlation will be driven by the top three points. Two of those are familial colorectal cancers, and the incidence quoted is the incidence in people with the relevant mutations; the third is basal cell carcinoma, which barely counts as cancer from a medical or public health viewpoint
If we leave out the familial cancers and basal cell carcinoma, the proportion explained drops to about 10%.
If we leave out put back basal cell carcinoma as well, something statistically interesting happens. The correlation shoots back up again, but only because it’s being driven by a single point. A more honest correlation estimate, predicting each point based on the other points and not based on itself, is much lower.
So, in summary: the “two-thirds of cancers explained” is Just Wrong. Doing a mathematically correct calculation gives about one third. Doing a calculation that’s actually relevant to cancer in the population gives even smaller values. (update) That’s not to say that DNA replication errors are unimportant — the paper makes it clear that they are important.
Thomas Lumley (@tslumley) is Professor of Biostatistics at the University of Auckland. His research interests include semiparametric models, survey sampling, statistical computing, foundations of statistics, and whatever methodological problems his medical collaborators come up with. He also blogs at Biased and Inefficient See all posts by Thomas Lumley »
2 large scale recent cancer media releases within 2 days at the beginning of the year just smacks of spin.
Cancer forecasts are for further increases in those cancers which have shown increase within the last decade.
Much of the EU is addressing EMF’s [banning wifi in schools in many countries]while other countries continue with the proliferation of radiations, and use of things like titanium dioxide in foods/soaps and the environment.
10 years ago
Can you point to an example of the EU ‘addressing’ wifi in schools?
10 years ago
I just googled ‘EU schools wifi’ and there is plenty of info. I think Germany France Scandanavia Switzerland and others, are all prohibiting the use of wifi and cell phones in schools. http://wifiinschools.com/uploads/3/0/4/2/3042232/europe_seeks_to_ban_mobile_and_wifi_in_schools.pdf
The UN has stated that emf’s are a possible class 2b carcinogen. http://en.wikipedia.org/wiki/List_of_IARC_Group_2B_carcinogens
along with coffee and talcum powders around the butt….
Some researchers are comparing the situation to lead, tobacco and asbestos, in regards to public opinion.
The International Agency for Research on Cancer (IARC; French: CIRC) is an intergovernmental agency forming part of the World Health Organisation of the United Nations.
http://en.wikipedia.org/wiki/International_Agency_for_Research_on_Cancer
10 years ago
The link on that PDF isn’t to a European Council document. It’s to a radio station in Spain, and the page doesn’t exist any more.
IARC has indeed said that EMFs (*not* WiFi) are a (Group 2b) possible carcinogen. As I’ve pointed out from time to time, 2b is essentially the lowest IARC category: IARC has only ever said one thing is probably *not* a human carcinogen, and the IARC classification deliberately takes no account of whether the actual levels of exposure are safe.
10 years ago
If you want the real Council of Europe (not EU, not the same thing at all) report from the Committee on the Environment, Agriculture and Local and Regional Affairs, it’s here:http://assembly.coe.int/ASP/Doc/XrefViewPDF.asp?FileID=13137&Language=EN
The committee adopted in in May 2011, which I think shows how much impact it’s having.
Since then, France has adopted a stricter standard on EMF dose from WiFi, but this standard allows for a lot more EMF than current WiFi actually produces.
10 years ago
How did the authors of the study choose which cancers to include in the graph? It strikes me as odd that breast and prostate cancers (for which there are plentiful data) were not included.
10 years ago
They needed data on stem cell numbers and division rate, not just on incidence.
10 years ago
Thanks for an insightful reanalysis.
In your third-to-last paragraph, beginning “If we we leave out the familial cancers and basal cell carcinoma…,” did you mean to include basal cell carcinoma in the sentence? I ask because your next paragraph then starts, “If we leave out basal cell carcinoma as well…,” which leaves your point confusing.
10 years ago
First I leave out all three, then I put basal cell carcinoma back in. Thanks for pointing out the editing error — I’ve updated.
10 years ago
(Not directly related but quite interesting) … I was watching QI the other night and Stephen Fry said that the blue whale have 2 thousand times more cells than humans so you’d expect blue whales to have a higher cancer rate (because of more transcription errors) but they actually have less.
It was called Peto’s Paradox – http://en.wikipedia.or/wiki/Peto%27s_paradox
10 years ago
This may actually be the point of looking at stem cells rather than total cells — though I don’t expect the data on cancer incidence in blue whales is as good.
10 years ago
Since you have pulled out the raw data, which does not appear to be normally distributed by eye, what is spearman’s Rho for these correlations?
10 years ago
I don’t have the data with me, but I’ll look it up when I get home. Spearman’s rho will be quite high, I should think.
10 years ago
Spearman’s rho is 0.81.
I’m not sure that’s very helpful — there isn’t a very good ‘variation explained’ interpretation of Spearman’s rho, and the interpretation for the ordinary r-squared has nothing to do with the Normal distribution.
In case anyone’s curious, Kendall’s tau is 0.63
10 years ago
My problem with the piece is that explained variance is not the same thing as causal importance at all.
10 years ago
That’s true in general. In this case, however, there’s less potential for confounding than usual — it isn’t very plausible that some other factor is separately affecting both cancer incidence and number of stem cell divisions, in the same way across a wide variety of cancers.
10 years ago
True.
Consider the following hypothetical possibility: absent certain environmental triggers, there would be very little cancer in any tissue. But if a population of people is exposed to those triggers, the rate of cancer rises in proportion to how much cell division is occurring. If all of that is the case, then while cell division is related to cancer incidence, it would be a complete non sequitur to say that those cancers were due to bad luck — get rid of the environmental triggers and the rates of all cancers drop back to near zero.
Not saying that’s the case, just that explained variance cannot tell us about the relative causal importance here.
10 years ago
Yes, that’s possible. It’s even known to happen to some extent — that’s the old distinction between initiators and promoters in cancer epidemiology. However, I think it’s relatively implausible that something of that sort acts uniformly across cancer types. Especially as we know that even faulty DNA mismatch repair genes don’t act uniformly across cancer types. I’m not saying it’s inconceivable, just that it’s sufficiently unlikely to make this evidence worth considering.
10 years ago
Suppose there were a set of genes that effectively created 10 types of people with varying levels of susceptibility to flu. (1 = not susceptible at all, 10 = any flu puts you in the hospital or kills you).
But the flu vaccine works pretty well, and so out of 10 people, only 1 or 2 get the flu, and it’s not always the ones with the greatest susceptibility. So an analysis might find, “These genes predict little of the variability in the flu.”
Conversely, if the flu virus is present and there is no vaccine, everyone gets the flu in the exact amount predicted by the genes. So an analysis would say, “These genes predict all of the variance in flu.”
But in neither case is the predicted variance really telling you the right answer about the causal relationship between genes, virus, and vaccine (which is very simple compared to cancer).
10 years ago
Your claim that “The proportion of variation explained is 18% and 28% respectively.” is misleading. The distribution of incidence is skewed. r-square is very sensitive to skewness. Therefore calculating r-square on the non-transformed data is meaningless (even after discarding outliers).
It would be great if you elaborate on the ” more honest correlation estimate”.
10 years ago
Sorry, it’s just not the case that r2 becomes meaningless in some way when the distribution is skewed. It may or may not become less useful, depending on what you’re using it for.
As long as you have a model with the right relationship between x and the mean of y, 1 – r2 always estimates the ratio of the variance of y conditional on x to the variance of y overall. That’s just algebra.
So, the two-thirds proportion of variation in log incidence explained by log(stem cell division), and the one-third variation in incidence explained by square root of stem cell divisions are both correct. They answer different questions, though. The question is which one answers the question you want to ask.
If you want to say something about what proportion of cancer cases in the human population could be due to stem-cell division errors, you need to look at incidence, not log(incidence). Another approach, if you are attached to the nice distribution of log(incidence) is to weight each observation by the incidence of that particular cancer type. That gives a proportion of variation explained of about 40%, before you start worrying about the familial cancers. I did that on my blog.
If you want to say something about how close the relationship is across different cancer types, the r^2 in the Science paper is fine. The problem is translating this into “two-thirds of cancer is due to bad luck”, as has been done in the press release and in a lot of media reports.
10 years ago
Update: What is true about outliers is that the choice of which cancers to include or not include will make more difference when the distribution has outliers.
In this case, it appears the researchers used all the cancers where they could find the right data.
10 years ago
Thanks for the detailed response.
The problem is in the sentence “As long as you have a model with the right relationship between x and the mean of y”. The mean of y is a bad estimator of y when the distribution is skewed or with outliers. So r-square on the raw incidence data is not very useful for estimating the amount of variation explained. The high correlation observed in the logarithmic scale suggests that rsquare on the non-transformed data is underestimation of the explained variation. This is also true when you use the square root of stem cell divisions in x.
The weighed method is probably better, and with this estimator 44% of variation are explained, still a lot of “bad luck”.
10 years ago
If we assume that there is a fixed probability of an oncogenic mutation at each cell dvision is fixed, then one might argue that the best model for incidence would be possion (probability of oncogenic mutation with a fixed time with the rate dependent on stem cell division rate). If this were the case, would expect a relationship between mean incidence and variance, and the log-scale would be the correct way to show the data, would it not? And in this case *if* there were a strong dependence of incidence on stem cell divisions, would expect the r^2 of the log plot to be high, but the r^2 of the non-log plot to be low.
10 years ago
It’s a perfectly good way to show the data — I said so, right at the beginning of the post. My point is about the claims for cancer cases in the population. The rare sarcomas have almost no impact on the total; it’s the common cancers that are responsible for most of the incidence. So, if you care about proportions of cancer cases in the population, as most of the media coverage does, you need the incidence scale.
10 years ago
Nobody seems to notice that lung cancer (smoker) is about 2.5 order higher than nonsmoker’s lung cancer. Is there stronger evidence for environmental cause of cancer? You may also see similar case in hepatocellular carcinoma due to hepatitis C virus and usual hepatoma.
10 years ago
Some forms of non-Hodgkin’s lymphoma are very clearly strongly environmentally triggered. Immunosuppressive therapy is particularly strongly associated with induced lymphoma. Also, many kinds of chemotherapy increase the risk of later cancers.
On another topic, this study is getting lots of attention in the press, with no indication of any statistical criticism. Do you know of anyone who is preparing an editorial/response for the journal itself or for a major news outlet?
10 years ago
No.
10 years ago
Thanks for doing this analysis but it is almost waste of time.
Often we see GOOD biology and BAD statistics (many biology papers); sometimes we see BAD biology and GOOD statistics (non-biologists analysing downloaded data) but this Vogelstein paper is BAD biology and BAD statistics.
The problem framing is so full of errors, many addressed here, that are not worth listing them all.
But there is a deeper flaw in the INTERPRETATION by readers and the press:
That cancer is bad luck – and the dismay at this fact. This comes from an overt deterministic world view and the magical thinking that we can determine the cause of cancer and avoid it.
The stochastic component in cancer is well recognized – it is nothing new. Cells play dice every time they divide and have evolved many near but not perfect mechanisms to contain the consequences of the really bad throws.
How often do we see cancer patients without ANY recognizable risk factors! Also: Some cancer appear with such stunningly invariant frequency across all countries in the world that a fully deterministic cause is unlikely because it wold reflect the different lifestyles, and genetic backgrounds.
Hence the attempt to quantify the contribution of “background” stochasticity is laudable, but the latter is not novel as the public response suggests – and the execution in this paper rather poor.
Whenever a stochastic component is mentioned in science and society there is an outcry in the public because many cannot stomach indeterminacy. But there is stochasticity almost everywhere. Life is constrained randomness.
10 years ago
A large source of the problem arises from a fairly subtle source: Science Magazine’s limitation of an Abstract to 125 words. The Vogelstein abstract is exactly 125 words. So he and his co-author must have agonized over which words to cut from their draft abstract – as all of us have done as we prepare such abstracts. An “easy” cut for them ended up being a horrible mistake. The fourth sentence in the abstract reads, “These results suggest that only a third of the variation in cancer risk among tissues is attributable to environmental factors or inherited predispositions.” The next sentence, in the draft, undoubtedly read something along the lines of, “The majority of this third of the variation is due to bad luck, that is, random mutations arising during
DNA replication in normal, noncancerous stem cells.” They unthinkingly deleted “this third of the bad luck” or whatever the exact text was, thinking that the antecedent was clear. However, the average reader will read the antecedent as “cancer risk” rather than as “variation”. There is lots of blame stemming from lots of places, but the arcane constraints Science Magazine places on manuscripts, particularly the 125-word limits on the Abstract, are in part to blame and could also be fixed by appropriate changes to the AAAS editorial policy.
10 years ago
That’s true, but I’m pretty sure most of the journalists didn’t get the story by reading the abstract in Science
10 years ago
Interesting analysis, Thomas.
Armitage & Doll [1] noted a power law between age and cancer incidence. Assuming mutation is a Poisson process, they stated that the slope on a log-log plot of age versus cancer incidence indicates the number of driver mutations required to acquire cancer. The initial paper suggested 6 driver mutations [1]. This idea was used in a recent PNAS paper by Tomasetti & Vogelstein, which stated 3 driver mutations for some cancers (e.g., Lung, Colon).
With this in mind, we might expect the slope of the log-log plot shown in this paper (divisions, a transformation of age, vs cancer incidence) to be similar (e.g., between 3-6). But it appears to be < 1; what may explain the discrepancy?
[1] http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2007940/
[2] http://www.pnas.org/content/112/1/118.abstract
10 years ago
I don’t really know. Here’s a few possibilities.
Firstly, the slope isn’t going to be the same with lifetime cumulative incidence as with age-specific incidence (though I think the simplest version of the argument would say it’s steeper, not flatter)
Also, there’s error in the predictor variable and imperfect fit (because environment does matter). Those will tend to lower the slope.
Finally, not all the mutations have to happen in normally-dividing stem cells — maybe you only need one mutation in a stem cell and you can then rely on the remaining ones happening in its progeny. For example, once you lose p53 or some of the mismatch-repair genes, anything can happen.
10 years ago